Basamak cevabı
Basamak cevabı
Giriş
Bu derste bir devrenin basamak yanıtını hesaplamaya çalışacağız.
Örnek devre
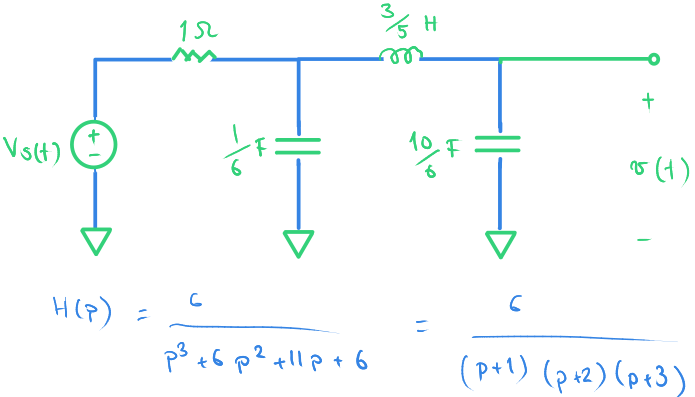
Yukarıdaki devrenin basamak cevabı soruluyor.
H(p) ile gösterilen devrenin aktarım işlevi. Bu işlevi çıkışın girişe oranı olarak düşünebiliriz.
Aktarım işlevi hazır olarak verilmiş.
Bazı devrelerde aktarım işlevi hazır olarak verilmeyebilir. Bizden aktarım işlevini bulmamız istenebilir.
Devre kaçıncı dereceden?
Bunu anlamak için enerji depolama elemanlarına ("sığaç ve bobinlere") bakmamız yeterli olacaktır.
Düğüm etrafında seri üç sığaç varsa devre ikinci derecedendir.
Bunun nedeni sığaçlardan iki tanesine bir gerilim değeri verdiğimizi düşünelim. Üçüncü sığacın gerilimi, Kirchoff gerilim kuralı gereği diğer iki sığacın gerilimine bağlı olacaktır. Birbirinden bağımsız iki ilk değer verebildiğimiz için devre ikinci derece olacaktı.
Bobinin sığaç gerilimlerine bir katkısı olmadığı için bu devre üçüncü derecedendir.
Kesirlere bölme
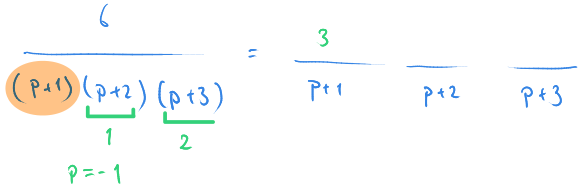
Devreyi çözmek için bu ifadeyi kesirli parçalara bölmek gerekiyor.
p+1 ifadesini elimizle kapattığımızı düşünelim. Bu ifadeyi 0'a eşitlediğimizde p+1=0 denkleminden p=-1 olarak buluruz.
İlk ifade kapalı iken bunu soldaki denklemde p yerine koyarsak, sağdaki denklemde ilk katsayıyı buluruz.
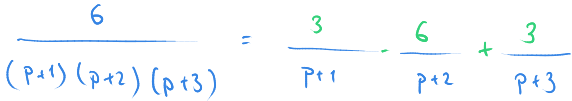
Diğer ifadeler için aynı yöntemi kullanarak sağdaki katsayıları bulabiliriz.
Elle çözüm
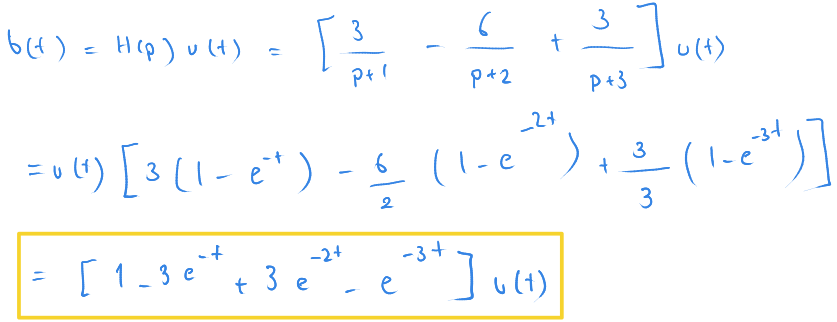
Devreyi elle çözersek sonuç yukarıdaki gibi olacaktır.
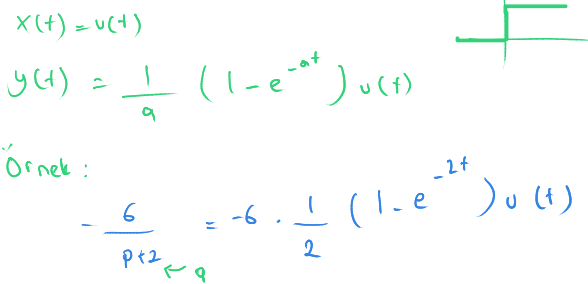
Eğer giriş basamak şeklinde ise, çıkışı hesaplamak için yukarıdaki formülü kullanabilirsiniz.
Sonucu sınayalım
Sonucu sınamak için, basamak cevabını matematik yazılımında çizdirebiliriz.
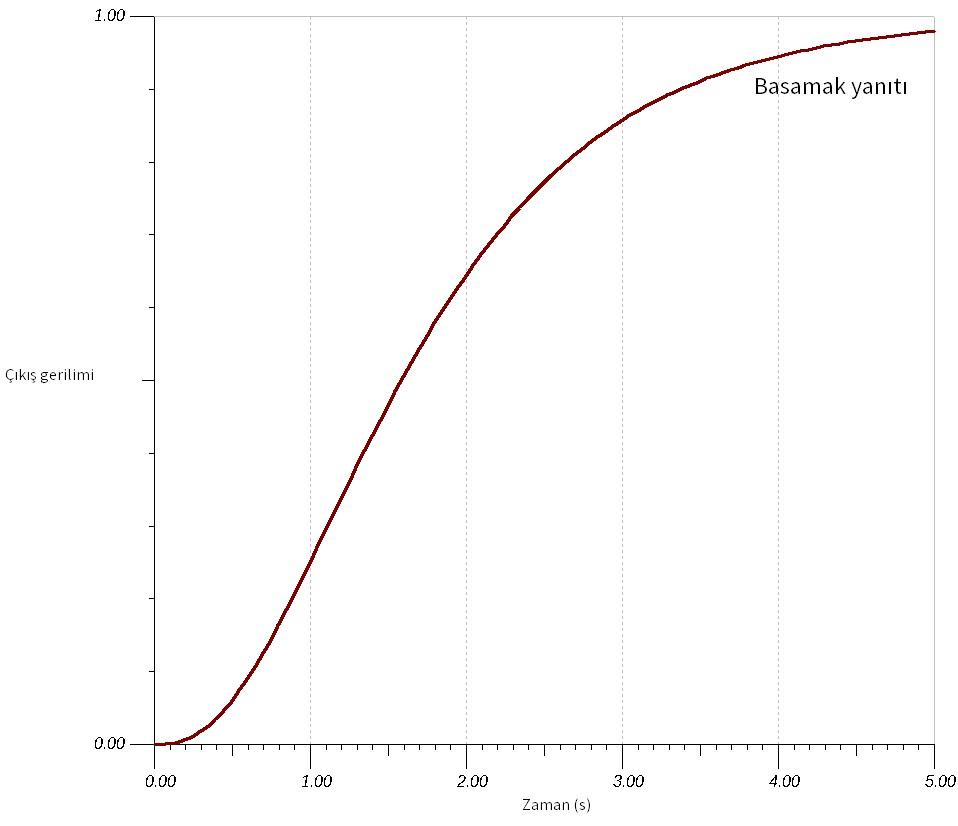
Benzetim yazılımı ile de benzer sonuçlar aldığımızı görebilirsiniz.
İsterseniz benzetim kütüğünü indirebilirsiniz.
Yorumlar