Birlik cevabı
Birlik cevabı
Hangi direnç
Elektronik alanında direncin çeşitli isimleri var.
Bunlara kısaca göz gezdirmekte fayda var.
Z = Tümdirenç Impedance
R = Direnç Resistance
X = Özdirenç Reactance
Y = Ters yüz direnç Admittance
R ile gösterilen direnç doğru akıma gösterilen zorluktur. X ile gösterilen öz direnç ise dalgalı akıma gösterilen mukavemettir.
Z ile gösterilen tüm direnç bu ikisinin toplamı bir karmaşık sayıya tekabül ediyor.
Y ise bunun ters yüz edilmiş hali gibi düşünebiliriz.
$\displaystyle{Y = \frac{1}{ Z}}$
Örnek devre
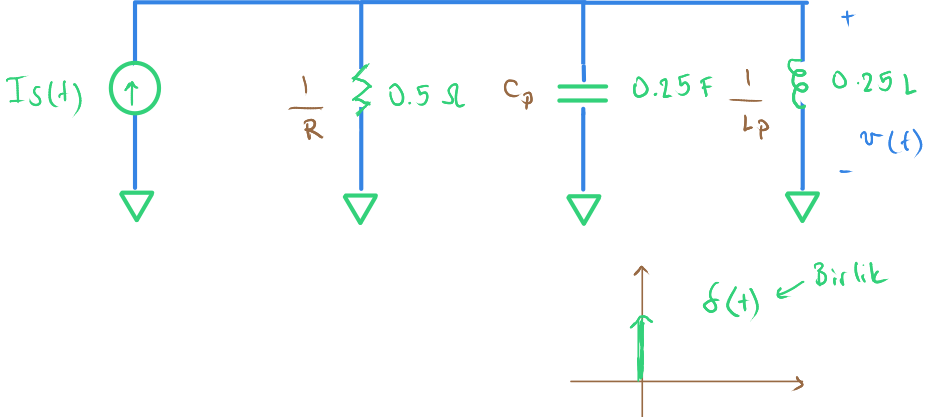
Yukarıdaki devrenin birlik yanıtı soruluyor.
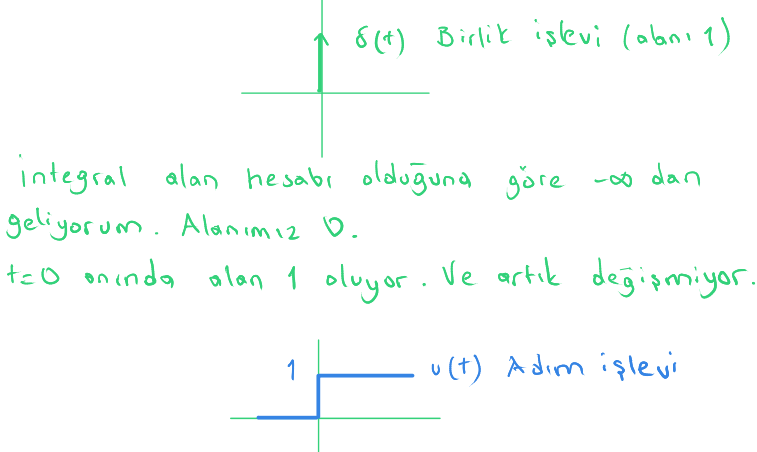
Birlik derken yukarıda gösterilen t=0 anında 1 sayısına benzer bir görünümü olan işareti kast ediyoruz.
Yukarıda $ δ(t) $ ile gösteriliyor ve alanının kuramsal olarak 1 olduğu kabul ediliyor.
Girişte birlik şeklinde bir akım uygulanıyor. Bize $ v(t) $ gerilimi soruluyor.
Devre denklemini yazalım
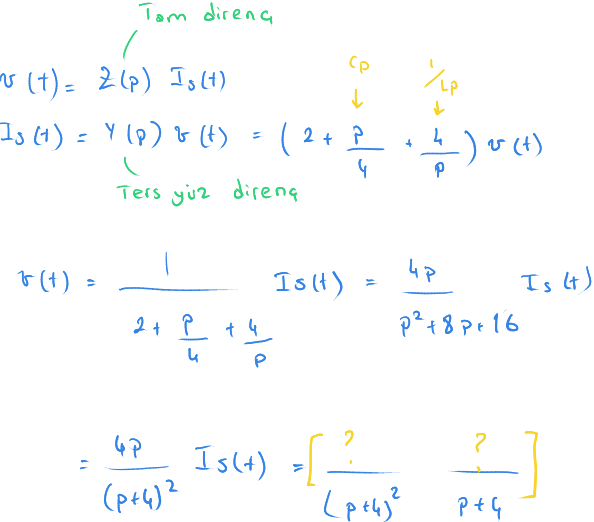
Öncelikle $ V = I . R $ olarak bilinen denklemi tam direnç ve ters yüz direnç türünden yazalım.
Burada ters yüz direnç kullanmamızın nedeni paralel elemanları basitçe toplayabiliyoruz.
Sığacın tam direnci $ \displaystyle { \frac {1} {Cp} } $ ile bobininki $ \displaystyle Lp $ oluyor.
Sığacın ters yüzdirenci $ \displaystyle { {Cp} } $ ile bobininki $ \displaystyle \frac {1} {Lp} $ oluyor.
Kesirlere bölme
Bu ifadeyi önceki derste olduğu gibi kesirlere bölmeliyiz.
Ancak altta ikinci dereceden bir ifade var.
Bu ifadeyi kesirlere bölmek için sırası ile aşağıdaki işlemleri yapıyoruz.
1 - ) İfadeyi $ ( p + 4)^2 $ ile çarp.
2 - ) $ p = -4 $ için sonucu bul. Bu $ ( p + 4)^2 $ nin katsayısını verecek.
3 - ) $ 4p $ 'nin türevini al. Bu $ ( p + 4) $ ün katsayısını veriyor.
Kısa şekilde Heaviside yöntemi ile çözümü aşağıda bulabilirsiniz.

Heaviside uzun çözüm
Heaviside yöntemi ile Laplace yönteminde olduğu gibi türevli denklemler çözülebiliyor.
Aşağıda çözümün uzun anlatımını bulabilirsiniz.

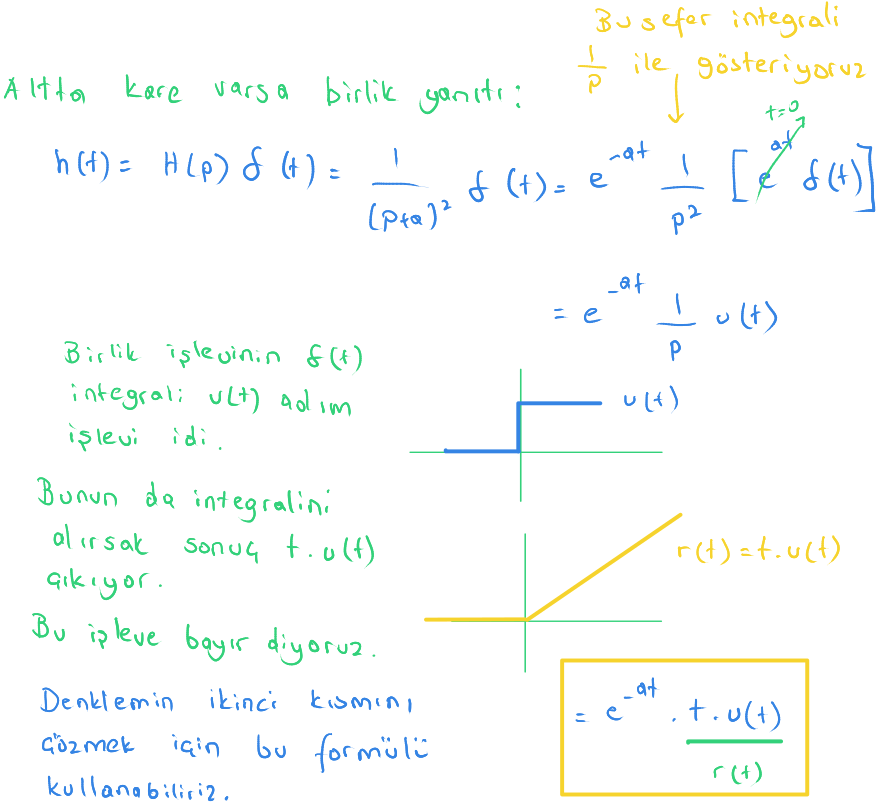
Yorumlar