Filtre uygulamaları
Filtre uygulamaları
Giriş
Bir önceki derste filtreler konusuna bir giriş yaptık.
Bu derste örnekler üzerinden konunun pekiştirilmesi amaçlanmıştır.
Alçak geçiren filtreler
Seri RL devre
Bobin ve dirençten oluşan bir devremiz olsun.
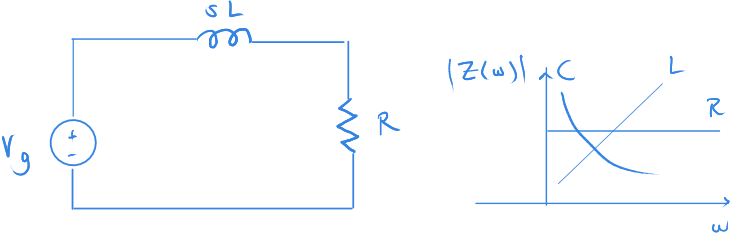
Girişte sinüs şeklinde zamanla değişen bir işaret olsun.
Sağ üstte, bazı devre elemanlarının tam dirençlerinin açısal dönüş sıklığına göre değişimi görülüyor.
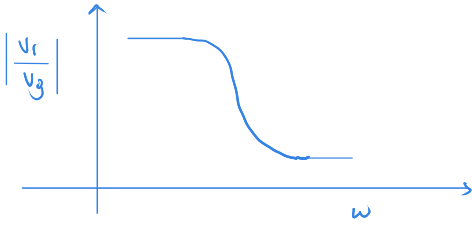
Buna göre çıkışın $ \Large {v_R} $ üzerinde olduğunu kabul ederek aktarım işlevini çizelim.
Yüksek sıklıklarda bobin açık devre gibi davranacak. Bu nedenle $ \Large {R} $ direnci üzerine az bir gerilim düşecek.
Alçak sıklıklarda ise bobin kısa devre gibi davranacak. Böylece tüm gerilim $ \Large {v_R} $ üzerine düşecek.
Çıkışta ise yüksek bir gerilim göreceğiz.
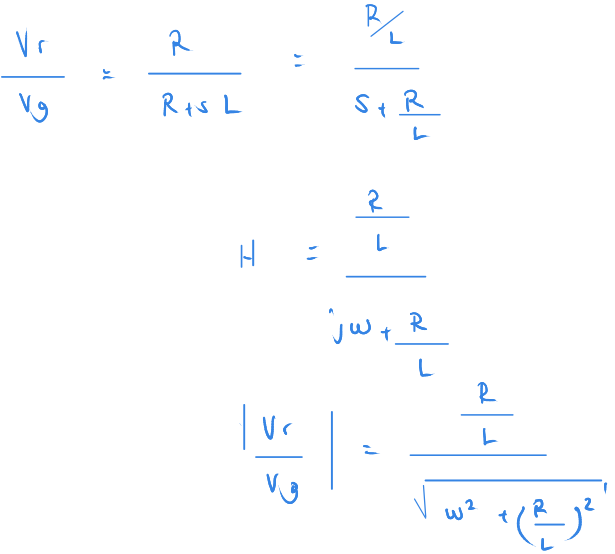
Aktarım işlevini her zamanki gibi hesaplıyoruz.
Bir sonraki adımda açı hesabı yapacağız.
Karmaşık sayılar
Karmaşık sayıları hatırlamakta fayda var.

Hatırlarsanız aktarım işlevi $ \large {H} $ harfi ile gösteriliyordu.
Çıkışın, girişe oranını veriyordu.
Yaptığımız örneklerde ise $ \large {|H|} $ ile gösterilen aktarım işlevinin vektörel büyüklüğünün ("mutlak değerini") açısal dönüş sıklığına bağlı $ \large {w} $ değişimini çizdik.
Yukarıda karmaşık sayı örneğimizde bunun karşılığının $ \large {r} $ olduğunu ve pisagor bağıntısından $ \Large {r = \sqrt{a^2+b^2}} $ olduğunu görebilirsiniz.
Karşının komşuya oranı $ \Large { tan \theta = \frac {b} {a} } $ diyebiliriz.
Sadece açı sorulursa $ \Large { \theta = arctan \frac {b} {a} } $ olur.
Açı hesabı
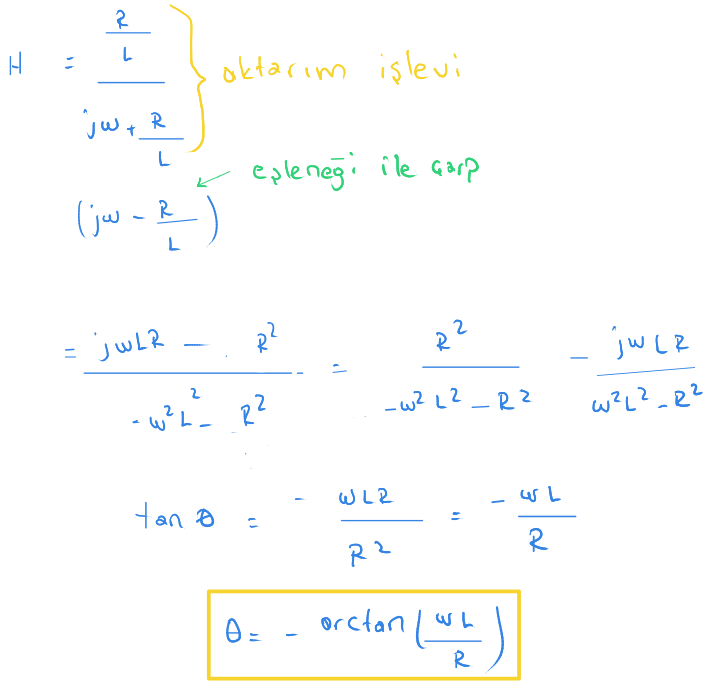
Açı hesabı yapabilmek için paydayı gerçel sayı haline getirmek gerekiyor. Bunun için karmaşık sayıyı eşleneği ile çarpıyoruz.
Açının açısal dönüş sıklığına göre değişimi
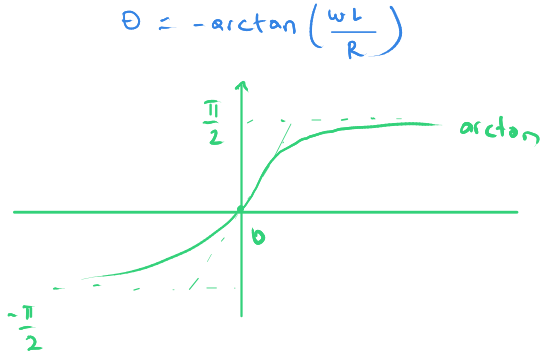
Açının açısal dönüş sıklığına göre değişimini çizebilmek için önce bulduğumuz açı değerini yazalım.
Yeşille gösterilen ise arctan işlevidir.
Açısal dönüş sıklığı $ \large {w = 0} $ iken açının değeri $ \large { arctan(0) = 0 } $ olur.
Açısal dönüş sıklığı $ \large {w = \infty} $ iken açının değeri $ \large { - arctan(\infty) = - \frac {\pi} {2} } $ olur.
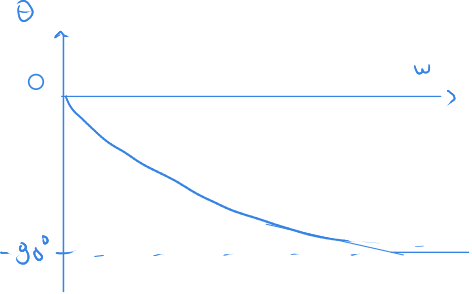
Bu bilgilere göre açının açısal dönüş sıklığına göre değişimini çizebiliriz.
Kesim sıklığı
$ \Large { |H_{kesim}| = \frac {1} {\sqrt{2}} H_{enyüksek} } $
Aktarım işlevinin vektörel büyüklüğünün, azalarak azami değerinin $ \Large { \frac {1} {\sqrt{2}} } $ sine düştüğü sıklığa kesim sıklığı diyoruz.
Seri RL devre kesim sıklığı
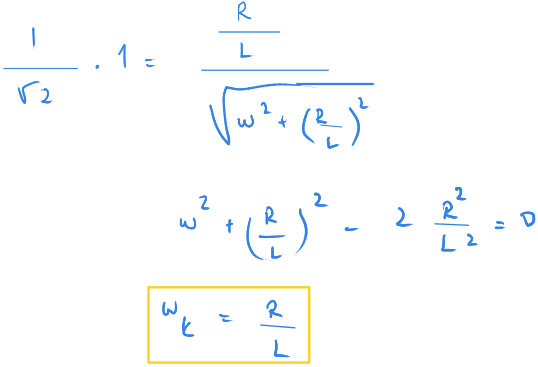
Yukarıdaki formülü kullanırsak kesim sıklığını $ \Large { w_{kesim} = \frac {R} {L} } $ buluruz.
Örnek
1 Hz ve civarı işaretleri geçiren, 10 Hz ve üzeri işaretleri söndüren filtre tasarlayınız. 1 Hz, 10 Hz ve 60 Hz sıklıklarında çıkışın vektörel büyüklüğünü hesaplayarak filtrenin sağlamasını yapınız.

Bobinin değerini 100 mH alırak direnci yaklaşık 6 ohm buluruz.

Kesim sıklığında çıkış işaretinin, giriş işaretinin vektörel büyüklüğünün $ \Large { \frac {1} {\sqrt{2}} } $ sine düştüğüne dikkat ediniz.
Yorumlar