Filtreler
Filtreler
Basit bir filtre
Çok basit bir tane sığaç ("kondansatör") ve dirençten oluşan bir devremiz olsun.
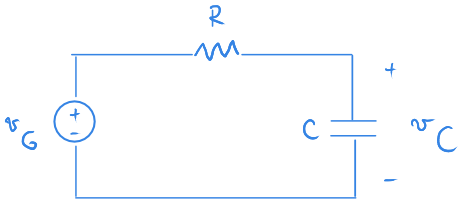
$ \Large {v_G} $ gerilim kaynağından sinüs şeklinde bir işaret uygulayalım.
Amacımız ise sinüs şeklinde bu işaretin sıklığı değiştikçe, sığacın uçları arasındaki $ \Large v_C $ gerilimini gözlemlemek olsun.
Devre elemanlarını tam direnç karşılıkları ile değiştiriyoruz.
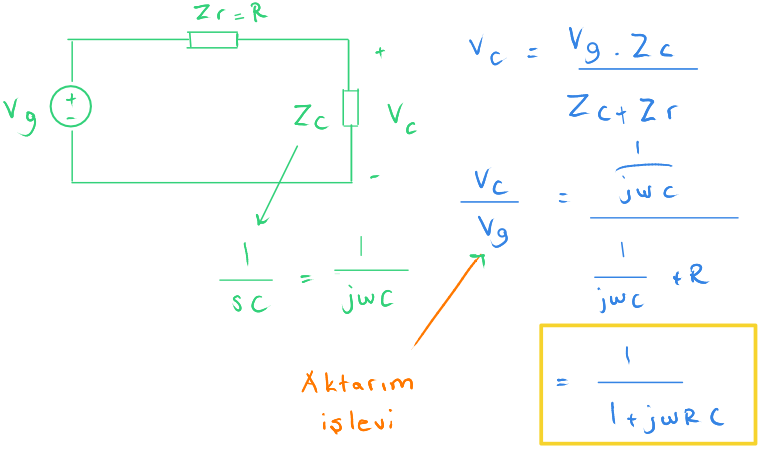
Tam direnç derken bir devre elemanının hem doğru, hem dalgalı akıma gösterdiği mukavemetin tamamına diyoruz.
Direncin tam direnci $ \large {Z_r\ =\ R} $ değişmiyor.
Sığaç için ise $ \Large {\frac {1}{sC} } $ ye eşittir. Burada $ \large {s\ =\ jw} $ 'dir.
$ \large {w} $ ise açısal dönüş sıklığını gösteriyor.
Açısal dönüş sıklığı ile sıklık arasındaki bağıntı şu şekildedir.
$ \large {w = 2 \pi f} $
Örneğin sıklık 1 ise açısal hız saniyede bir tur ya da $ \large {2 \pi} $ radyandır.
$ \large {j} $ ye gelince bu karmaşık sayılardaki $ \large {i} $ sayısıdır. Akımla karışmaması için $ \large {j} $ harfi ile gösteriliyor.
Devre elemenlarını, tam direnç karşılıkları ile değiştirdikten sonra basit gerilim bölücü kuralını kullanabiliriz.
Buradan çıkış geriliminin, giriş gerilimine oranını hesaplıyoruz. Bu işleve aktarım işlevi adı veriliyor. $ \large {H} $ harfi ile gösterilebiliyor.
Alçak geçiren filtre
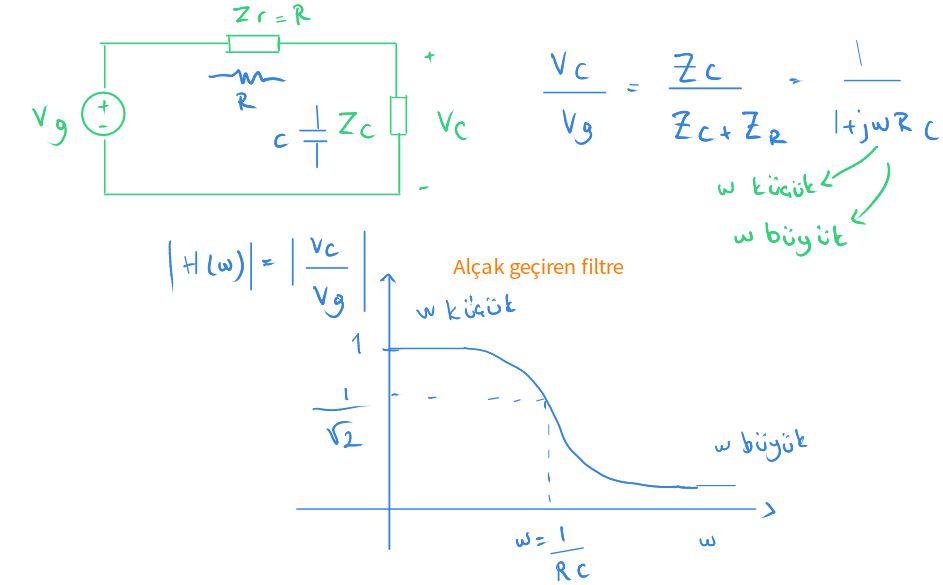
Aktarım işlevinin açısal dönüş sıklığına göre değişimini çizmek istiyoruz.
Eğer açısal dönüş sıklığı $ \large {w} $ küçük ise aktarım işlevinde alttaki $ \large {jwRC} $ değerini göz ardı edebiliriz.
Bu durumda aktarım işlevinin değeri 1 çıkar.
Sonucun bir çıkması demek, girişteki sinüs şeklindeki işareti çıkışta da bozulmadan görmek anlamına geliyor.
Eğer açısal dönüş sıklığı $ \large {w} $ büyük ise aktarım işlevinde alttaki bir değerini göz ardı edebiliriz.
Bu durumda aktarım işlevinin mutlak değerini alırsak $ \Large { \frac {1} {wCR} } $ olur.
Yani sonuç küçük bir değer çıkar.
Bu da açısal dönüş sıklığı yüksek olduğu durumda çıkış işaretinin söndüğü anlamına geliyor.
Burada aktarım işlevine $ \Large {\frac {1}{1+jwRC} } $ baktığımızda eğer $ \Large { w = \frac {1} {RC} } $ dersek bu durumda aktarım işlevinin mutlak değerini $ \Large { \frac {1} {\sqrt {2} } } $ buluruz.
Bu filtreye düşük sıklıklı işaretleri geçirip, yüksek sıklıklı olanları söndürdüğü için alçak geçiren filtre deniliyor.
Tam dirençlerle işlemler
Bu bölümde tam dirençlerle nasıl işlem yapıldığına bakalım.
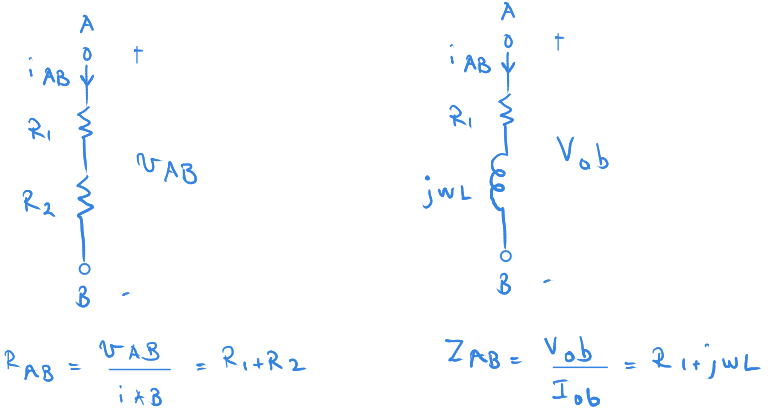
İlk örneğimiz seri dirençlerden oluşuyor.
Bu durumda tam direnç bu iki direncin toplamına eşit oluyor.
İkinci örnek ise bir direnç ve bobinden oluşuyor.
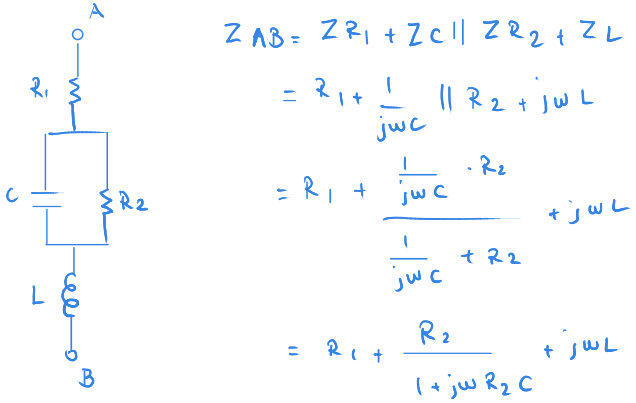
Son örneğimiz ise her üç devre elemanını içeriyor.
Başka filtreler tasarlayalım
Sizle öyle bir ipucu paylaşacağım ki neler yapıldığını görünce şaşırabilirsiniz.
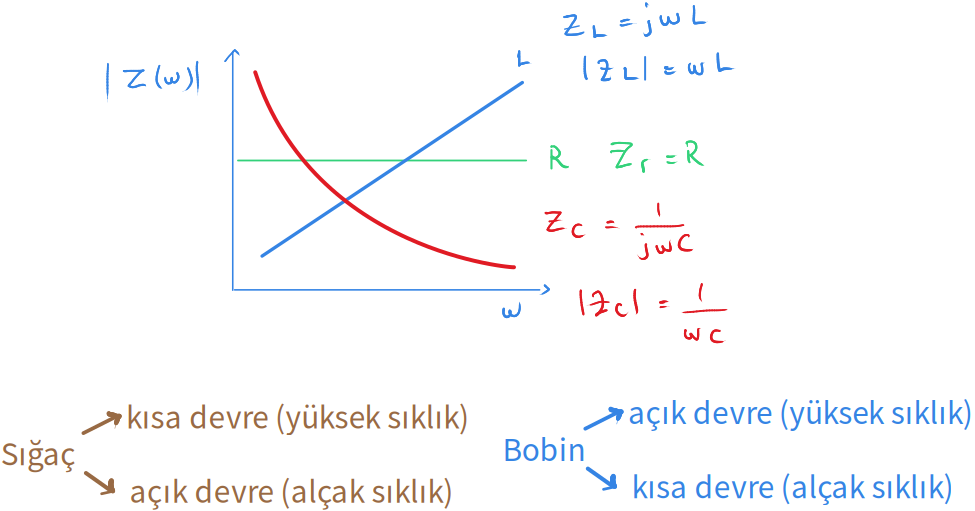
Burada üç tane temel devre elemanının tam direncininin, açısal dönüş sıklığına göre $ \large {w} $ değişimi görülebiliyor.
Direncin tam direnci değişmeden sabit kalıyor.
Sığaca ("kondansatör") baktığımızda ise düşük sıklıkta açık devre, yüksek sıklıkta ise kısa devre davranışı gösteriyor.
Düşük sıklığa örnek doğru akım verilebilir. Gerçekten de sığaç doğru akımı geçirmez.
Sıklık arttığında ise kısa devre gibi davranıyor.
Bobinin davranışının ise sığacın tam tersi olduğu görülebilir.
Yüksek geçiren filtre
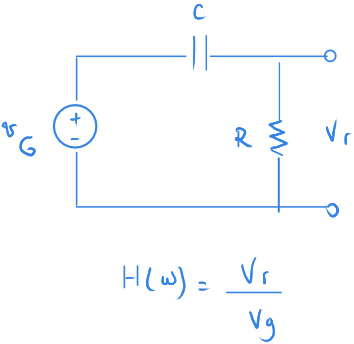
Örnekte direnç üzerindeki gerilim bizim çıkışımız olacak.
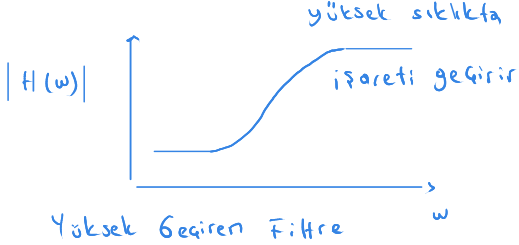
Açısal dönüş sıklığı yüksek iken sığac kısa devre davranışı gösterecek. Bu durumda sığacı bir telle değiştirdiğinizi düşünebilirsiniz.
Bu durumda $ \Large {V_{i}} $ giriş geriliminin tamamı $ \Large {V_{r}} $ çıkışında görüleceği için yüksek sıklıkta çıkış ve dolayısıyla aktarım işlevi yüksek bir değer alacak.
Düşük sıklıkta ise sığaç açık devre özelliği gösterecek. Bu durumda giriş ucundan çıkış ucuna çok az bir akım akabilir. Dolayısıyla aktarım işlevi küçük bir değer alacak.
Bu filtreye yüksek sıklıklı işaretleri geçirip, alçak sıklıklı olanları söndürdüğü için yüksek geçiren filtre deniliyor.
Alçak geçiren filtre
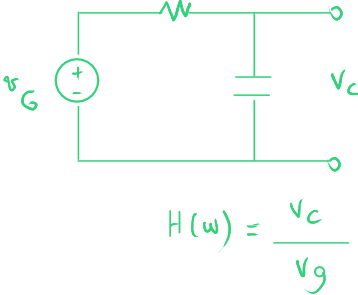
Bu örneği hatırlayabilirsiniz.
Ancak pratik yöntemi göstermek maksadıyla tekrar üzerinden geçiyoruz.
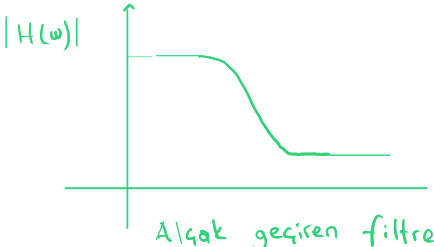
Sığaç yüksek sıklıkta kısa devre özelliği gösterdiği için $ \Large v_C $ gerilimi küçük bir değer olacak.
Düşük sıklıkta ise açık devre özelliği gösteriyordu ve doğru akımı engelliyordu.
Bu nedenle $ \Large v_C $ uçları açık iken giriş gerilimi çıkışta görülecek.
Yüksek geçiren filtre
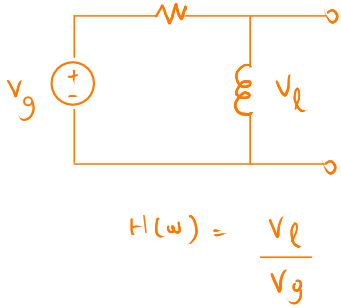
Örneğimiz direnç ve bobinden oluşuyor.
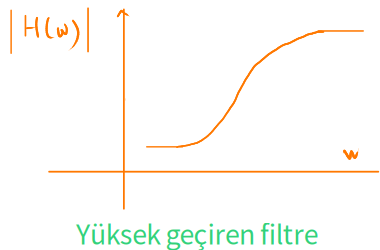
Bobin düşük sıklıkta kısa devre davranışı gösterdiği için çıkış gerilimi neredeyse sıfır olacak.
Yüksek sıklıkta açık devre davranışı gösterdiği için giriş gerilimi bobin üzerinde $ \Large v_L $ görülecek.
Band geçiren filtre
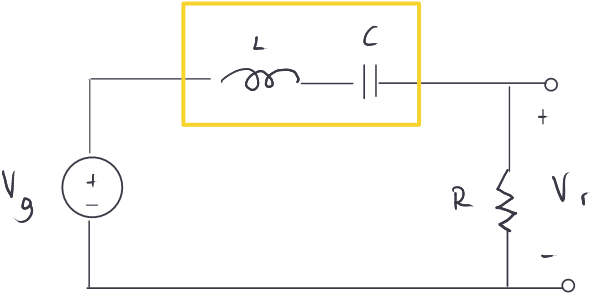
Devremiz üç tane devre elemanını da içeriyor. Dikdörtgen içine alınmış bölüme dikkat ediniz.
Bu devrede çıkışımız direnç üzerindeki $ \Large V_r $ gerilimi olacak.
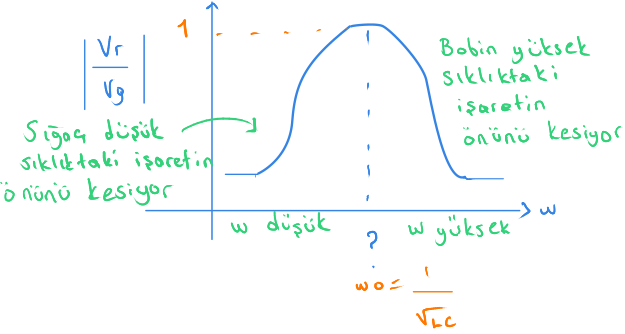
Tekrar sarı dikdörtgen içine alınmış bölüme dönelim.
Eğer dikkat ederseniz düşük ya da alçak sıklıklarda, bobin ya da sığaçtan birisi açık devre davranışı gösteriyor.
Böylece hem alçak hem de yüksek sıklıktaki işaretler engelleniyor.
Orta sıklıktaki işaretler için ise yukarıdaki durum oluşuyor.

Tekrar kalemi elimize alıp aktarım işlevini hesapladık.
Peki açısal dönüş sıklığını $ \Large {w = w_{0} = \frac {1}{ \sqrt{LC} } } $ alırsak ne olur?
Eğer hemen üstte sarı dikdörtgen içine alınmış aktarım işlevine bakarsanız karekök içindeki ifadenin sol kısmında bir eksi bir sıfır kalır.
Böylece ifade $ \Large {\frac {wRC}{ \sqrt{1 - 1 + (wRC)^2} } } $ halini alır.
Bu ifadeyi de sadeleştirdiğimizde sonuç $ \Large {\frac { |V_r |}{ |V_g|} = 1 } $ olur.
Aktarım işlevinin mutlak değerini bir yapan $ \Large {w_{0} = \frac {1}{ \sqrt{LC} } } $ açısal dönüş sıklığına yankılaşım sıklığı adı veriliyor.
Band durduran filtre
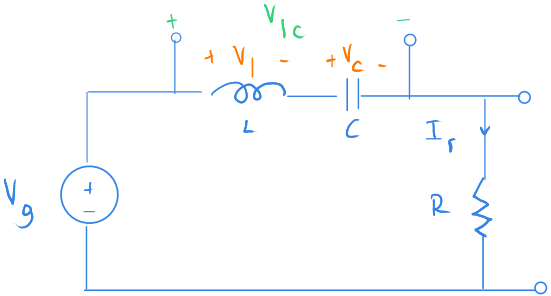
Devremiz band geçiren filtrenin aynısıdır.
Tek farkla ki bu sefer bobin ve sığacın gerilimini çıkış kabul ediyoruz.
Eğer dikkat ederseniz, sığaç ya da bobinden birisi düşük ve yüksek sıklıkta açık devre özelliği gösteriyor.
Böylece giriş gerilimi $ \Large V_{lc} $ arasında birikiyor. İleri geçemiyor.
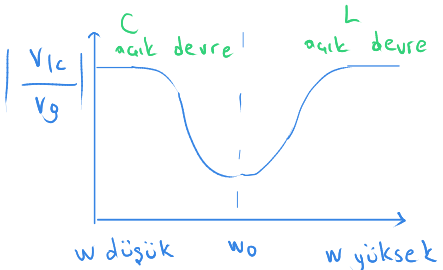
Yankılaşım sıklığında ise yukarıdaki durum ortaya çıkıyor.

Yankılaşım sıklığında ilginç bir durum ortaya çıkıyor.
Bobinin gerilimi ve sığaçın gerilimi birbirine eşit oluyor.
Ama gerilim zıt yönde oluştuğu için birbirlerini sıfırlıyorlar.
Başka bir örnek
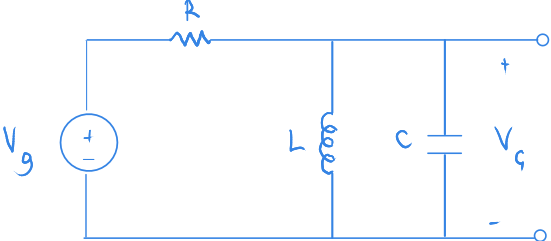
Bu örneğimizde düşük ve yüksek sıklıkta bobin ve sığaçtan biri kısa devre özelliği gösteriyor.
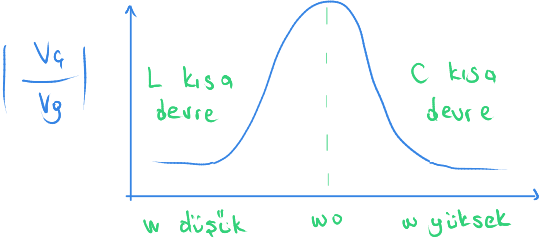
Böylece bant geçiren bir filtre oluşturmuş olduk.
AM radyo alıcısı
Şimdi dikkate değer bir filtre uygulamasına geçelim.
Bu devre AM radyo alıcısıdır.
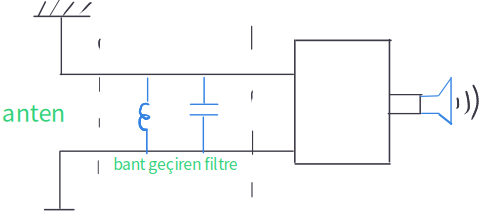
Bir tane anten, hemen altında bir toprağımız var.
Antenden bir işaret alıyoruz.
Antenden sonra sığaç ve bobinden oluşan ufak bir filtre takıyoruz.
İşareti çözüp, yükselttikten sonra sesi hoparlöre iletiyoruz.
Anten bir işaret alıyor. Sonra bir şekilde devrenin anten kısmını bir gerilim kaynağı olarak görebiliriz.
Bu nedenle anten kısmını aşağıdaki gibi Thevenin eş değeri ile değiştirebiliriz.
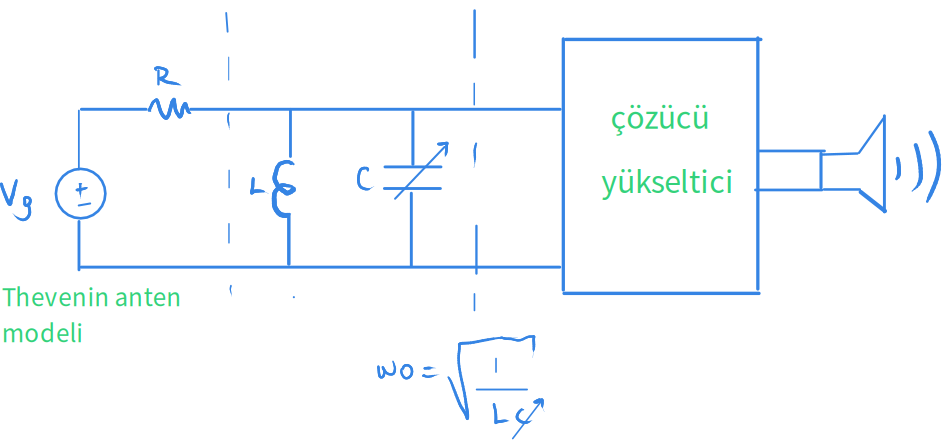
Devrenin son haline bakarsanız bunu bir önceki örnekte görmüştük.
Bu sefer kHz cinsinden yazalım.
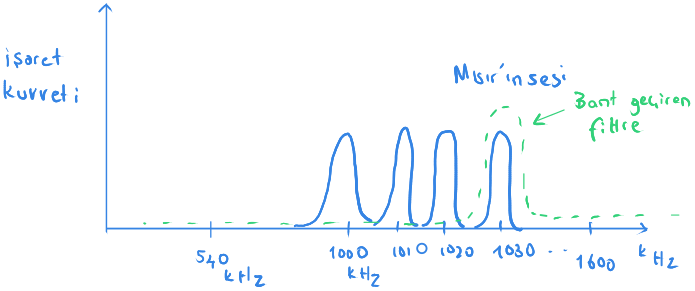
Bir yerleşim yerinde radyo işaretlerinin 540 kHz'den başlayıp 1600 kHZ'ye kadar gittiğini varsayalım.
Her radyo istasyonuna da 10 kHz yayın aralığı verildiğini varsayalım.
Her radyo da kendisine tahsis edilen sıklığın +5 kHz ya da -5 kHz etrafında yayın yapıyor olsun.
1030 kHz sıklığında Mısır'ın Sesi radyosu yayın yaptığını varsayalım.
Dikkat ederseniz yayın yapan tüm bu radyolara bir bant genişliği tahsis edilmiş.
Bir radyoyu nasıl dinlersiniz?
Bir radyoyu dinlemek için işaretin tamamını bant geçiren bir filtreden geçirelim.
Filtremizin $ \large {w} $ açısal dönüş sıklığını ise 1030 kHz'ye ayarlarsak sadece Mısır'ın Sesi radyosunu seçip, diğerlerini göz ardı etmiş oluruz.
Yorumlar