Heaviside yöntemi 1
Bu derste Heaviside yöntemine giriş yapacağız
Giriş
Bu derste türevli denklemleri çözmek için Heaviside yöntemini kullanmaya çalışacağız.
Öncelikle tabloya bakalım.
Heaviside tablosu


Açıklama
Bir tane sistemimizin olduğunu düşünelim.

$ x(t) $ sistemin girişi $ y(t) $ çıkışı olsun. Birlik cevabı ise $ h(t) $ olsun.
Bu durumda çıkışı şu şekilde yazabiliriz.
$ y(t) = x(t) * h(t) $
Aradaki asteriks işareti türetme integrali ("convolution") anlamına geliyor.
Bir de $ h(t) $ ile ilişkili sistem işleci var.
Sistem işleci $ H(p) $ ile gösteriliyor.
$ y(t) = H(p)\ x(t) $
$ x(t) $ üzerinde işlem yapar ve $ y(t) $ yi üretir.
Bir diğer ifade ile sistem işleci giriş üzerinde işlem yapar ve çıkışı üretir.
Şimdi şöyle bir soru soruyoruz.
$ x(t) $ yi daha basit bir şey cinsinden üretebilir miyiz?
İntegral almayı çok kolaylaştıran bir işlev var. Çünkü bir nokta dışında değeri sıfır.
Bu işlev birlik işlevi ve $ δ (t) $ ile gösteriliyor.
$ x(t) $ yi birlik cinsinden yazabilir miyiz?
$ x(t) = X(p)\ δ(t) $
$ x(t) $ yi üreten $ X(p) $ işleci nedir?
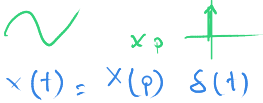
Bir tane birlik alıyor. Onun üzerinde işlem yapıyor. $ x(t) $ dalga şeklini üretiyor.
Bu işleç nedir? Neden faydalıdır?
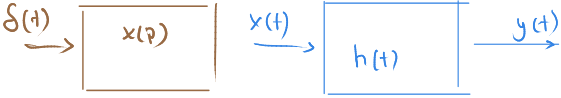
$ X(p) $ burada başka bir sistem varmış gibi $ x(t) $ yi $ δ(t) $ den üretiyor.
Sanki iki sistem birbirine bağlanmış.
Eğer giriş için bunu yazabilirsem,
$ x(t) = X(p)\ δ(t) $
benzer bir ifadeyi çıkış için de yazabilirim.
$ y(t) = Y(p)\ δ(t) $
Bu iki işleç dalga biçimlerini bir birlikten üretiyorlar.
Bir tane birlikle başlıyoruz. En sonunda dalgayı üretiyorlar.
Tabloya geri dönelim
Artık tabloya bakabiliriz.
Tablonun sol kısmı bir işlevi gösteriyor. Sağ kısmı ise bu işlevi $ δ(t) $ den üreten işleci gösteriyor.
Tablodaki ilk kayıt olan $ x(t) = \ δ(t) $ ye bakalım. Bu işlevi üreten işleç nedir?
$ \displaystyle { 1 }$
Çünkü bakarsanız giriş de birlik işlevi idi.
İkinci kayda baktığımızda $ x(t) = \ u(t) $ olduğunu görebiliriz.
Basamak şeklinde bir dalgayı birlikten nasıl üretebilirsiniz?
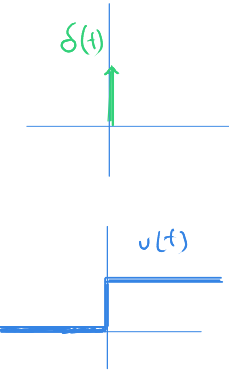
İntegral alma alan hesabıydı.
Eksi sonsuzdan birliğe geliyoruz. Alan sıfır.
$ t = 0 $ iken birliğin alanı 1 oluyor. Artı sonsuza doğru devam ettiğimizde alan 1 olarak kalıyor.
Demek ki birlik işlevinin integrali, basamak işlevini $ u(t) $ veriyor.
İntegral işlemini tabloda $ \displaystyle{ \frac {1} {p} } $ ile gösteriyoruz.
Örnek
$ \displaystyle { \frac {1} {p} [ sin\ 5t\ u(t) ] \ = \ ? } $
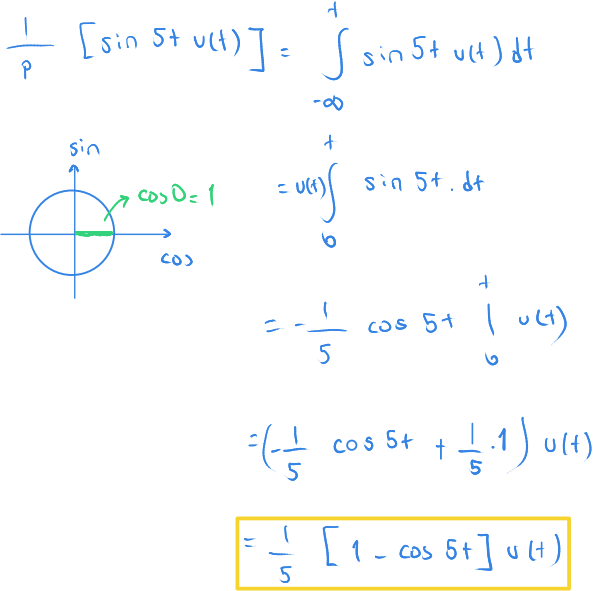
Burada $ t $ ve $ {-\infty} $ aralığından nasıl $ t $ ve $ 0 $ aralığına geldik diye düşünülebilir. Basamak işlevinin $ {-\infty} $ ve $ 0 $ aralığında değeri $ 0 $ olduğu için, çarpım durumundaki bu ifade de $ 0 $ olacaktır.
Bu nedenle bu integrali $ t $ ve $ 0 $ aralığına taşıyabiliriz.
Örnek
$ \displaystyle { \frac {1} {p} [ cos\ 5t\ u(t) ] \ = \ ? } $
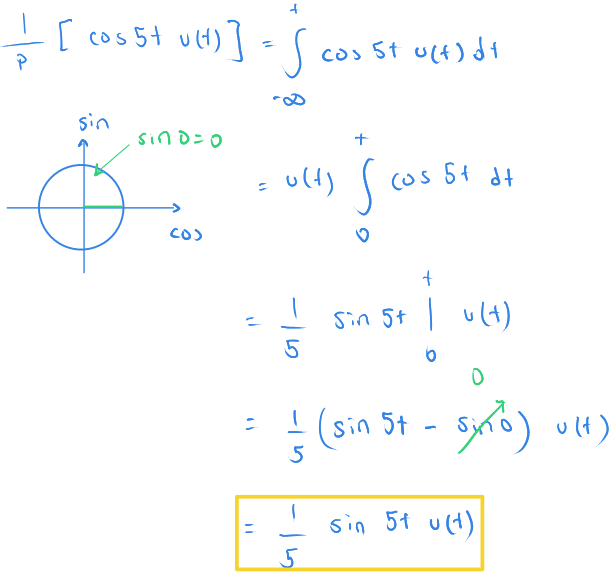
Yokuş işlevi
Tabloda üçüncü satırdaki $ r(t) = t\ u(t) $ yokuş işlevini gösteriyor.
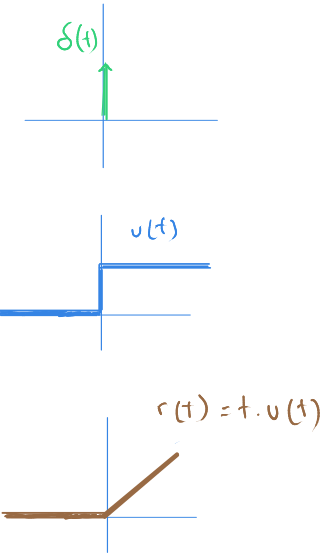
Birliğin integralini alınca basamağı veriyor. Basamağın integralini alınca yokuş işlevini veriyor.
Gerçekten de basamağın alanını hesaplayınca yokuş verdiğini matematik yazılımı ile de sınayabilirsiniz.
Burada işlecin $ \displaystyle { \frac {1} {p^2} } $ olduğuna dikkat ediniz. Bu ifade iki kere integral al anlamına geliyor.
Yorumlar