İkinci dereceden türevli denklemler
İkinci dereceden türevli denklemler
Giriş
Heaviside yöntemi ile ikinci dereceden türevli denklemler çözülebiliyor.
Örnek olarak bu sayfada sorulmuş bir soruyu çözmeye çalışacağız.
Örnek
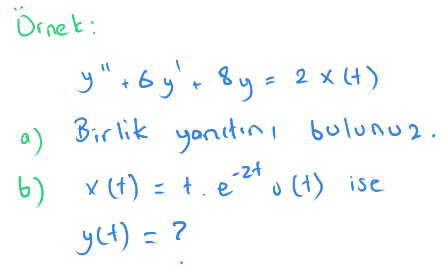
Burada bir tane ikinci dereceden türevli denklem verilmiş.
İlk şıkta birlik yanıtını soruyor.
Birlik derken darbe şeklinde alanı 1 birim olan, t=0 zamanında yukarı doğru bir sıçrama yapan bir işareti kast ediyoruz.
Birlik cevabı

İkinci dereceden türevli denklemin birlik yanıtını yukarıda bulabilirsiniz.
İntegral alan hesabı olduğu için eksi sonsuzdan gelip birlik işlevinin alanını hesaplarsak 1 olur.
Birlik işlevinin alanı, birim basamak işlevi u(t) olur.
Diğer şık
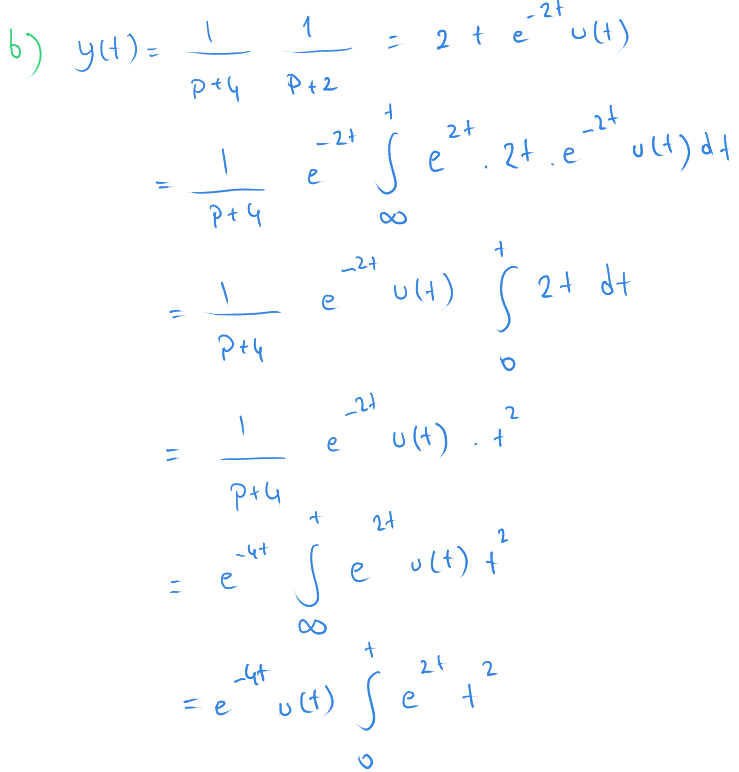
Buraya kadar türevli denklemi çözdükten sonra önümüze biraz değişik bir integral geldi.
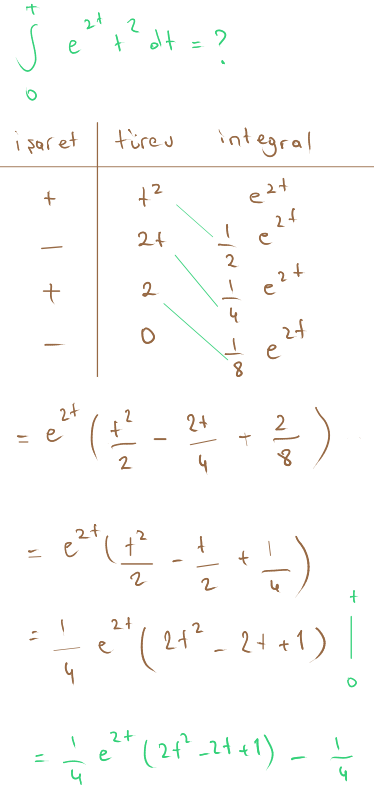
Kısmi integral yöntemi ile çözüyoruz.

Çözdükten sonra denklemde yerine koyabiliriz.
Kısa çözüm
Bu türevli denklemi Heaviside yöntemi ile daha kısa çözebiliriz.
Laplace dönüşümünde olduğu gibi tablolardan faydalanıyoruz.
Denklemin sağ tarafına da Heaviside yöntemi uyguluyoruz.
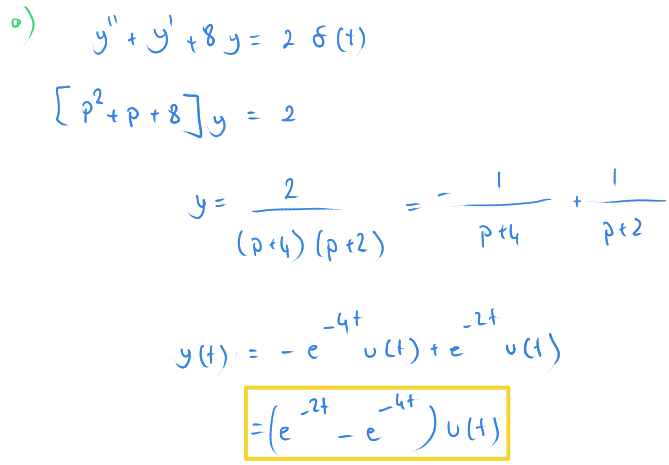
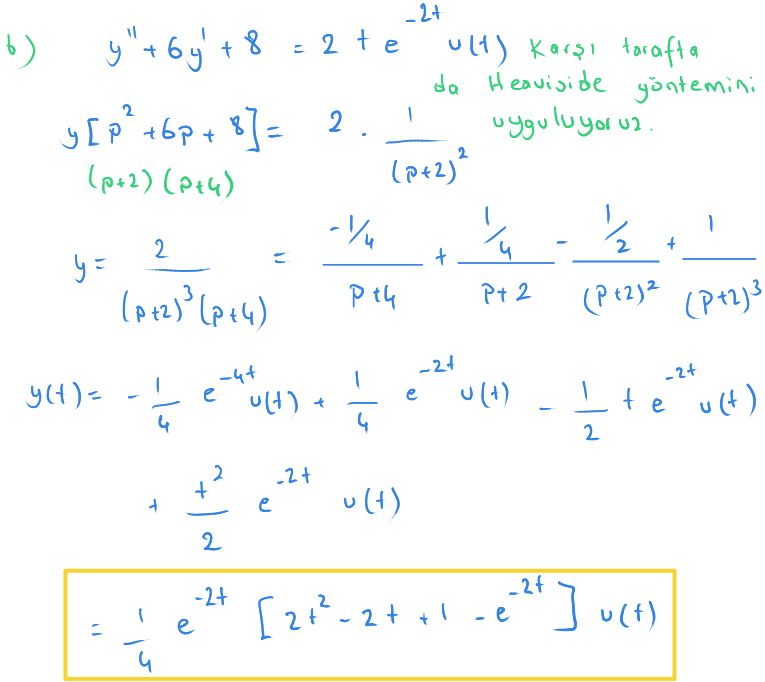
İkinci şıkta $ (p+2)^3 $ şeklindeki ifadenin nasıl kesirlere bölündüğünü ayrıca izah etmek gerekiyor.
Dikkat ederseniz tüm integral hesaplarını bir kenara bıraktık.
Yorumlar