Laplace dönüşümü
Laplace dönüşümü
Laplace dönüşümü
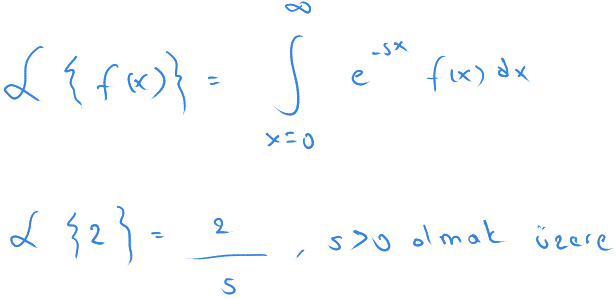
Laplace dönüşümü bir işlevi alıp bir çıktı üretiyor.
2 sayısının Laplace dönüşümü 2/s diyoruz.
Neden böyle olduğunu integrali çözerek görebiliriz.

e üzeri eksi sonsuzun 0 olduğuna dikkat ediniz.
Buradan k sabit bir sayı ise, Laplace dönüşümü k/s diyebiliriz. s > 0 olmak üzere.
Peki e^(-kx) in Laplace dönüşümü hakkında ne diyebiliriz?

Tekrar integrali çözelim.
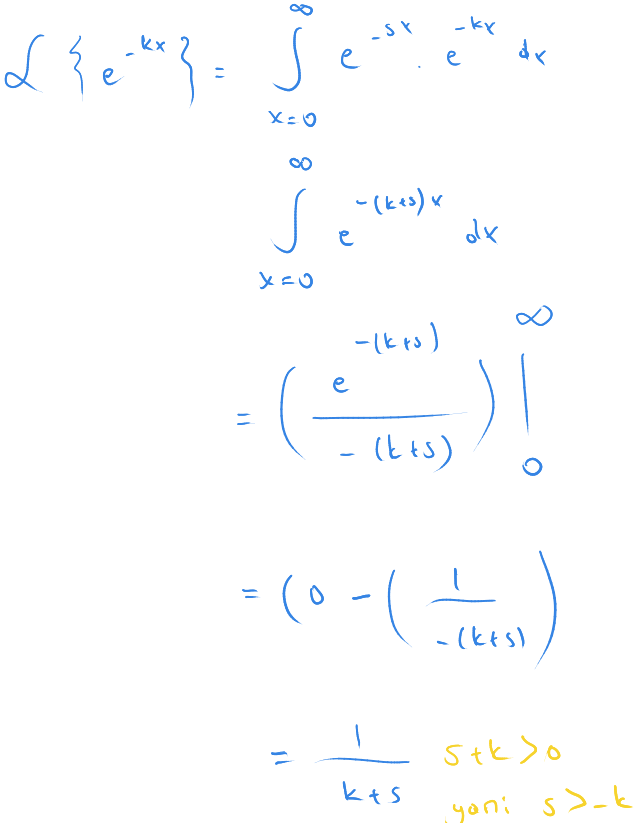
Laplace dönüşümünün tersi
Bir f(x) işlevinin Laplace dönüşümüne F(s) diyelim. Bazı durumlarda Laplace dönüşümü verilip, işlevin kendisi istenebilir.
Bu durumda f(x) Laplace dönüşümünün tersi olarak isimlendiriliyor.
İlk örnekte 2 sayısının Laplace dönüşümü 2/s demiştik.
Eğer F(s)=2/s ise bu durumda ters Laplace dönüşümü 2 olur.

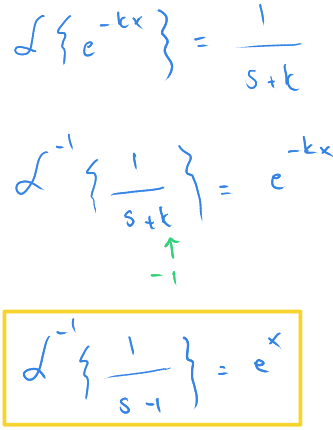
O zaman $F(s)=\frac{1}{s-1}$ 'in ters Laplace dönüşümü nedir?
Bunu yanıtlamak için bildiğiniz Laplace dönüşümlerine bakınız.
Laplace dönüşümü tablosu
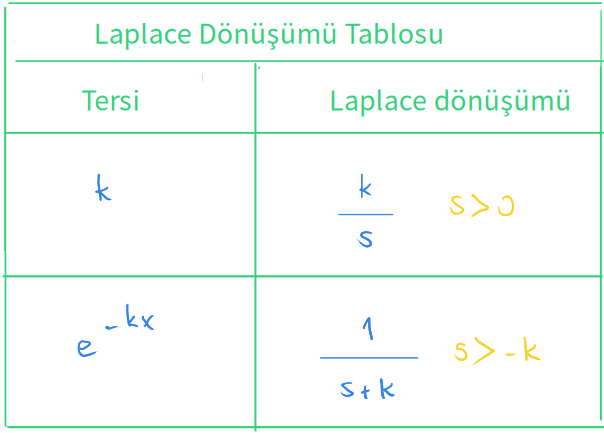
Tabloyu soldan sağa okuyarak Laplace dönüşümünü bulabilirsiniz.
Sağdan sola okuyarak ise ters Laplace dönüşümünü bulabilirsiniz.
Pekiştirme
Soruları çözerken mümkünse Laplace dönüşümü tablosunu kullanınız.
Eğer değilse temel Laplace ifadesini kullanabilirsiniz.
| 1-) Aşağıdakilerin Laplace dönüşümlerini bulunuz. Her örnekte f(x) $x>=0$ için tanımlıdır. | ||
| (a) f(x) = -3 | (b) f(x) = e | (c) $f(x) = e^{2x} $ |
| (d) $f(x) = -5e^{3x}$ | (e) $f(x) = 2e^{7x-2}$ | |
| 2-) Aşağıdakilerin ters Laplace dönüşümlerini bulunuz. | ||
| (a) $F(s) = \frac{-1}{s}$ | (b) $F(s) = \frac{1}{s-5}$ | (c) $F(s) = \frac{3}{s+2}$ |
| (d) $F(s) = \frac{-3}{4s}$ | (e) $F(s) = \frac{1}{2s-3}$ | |
Çözümler
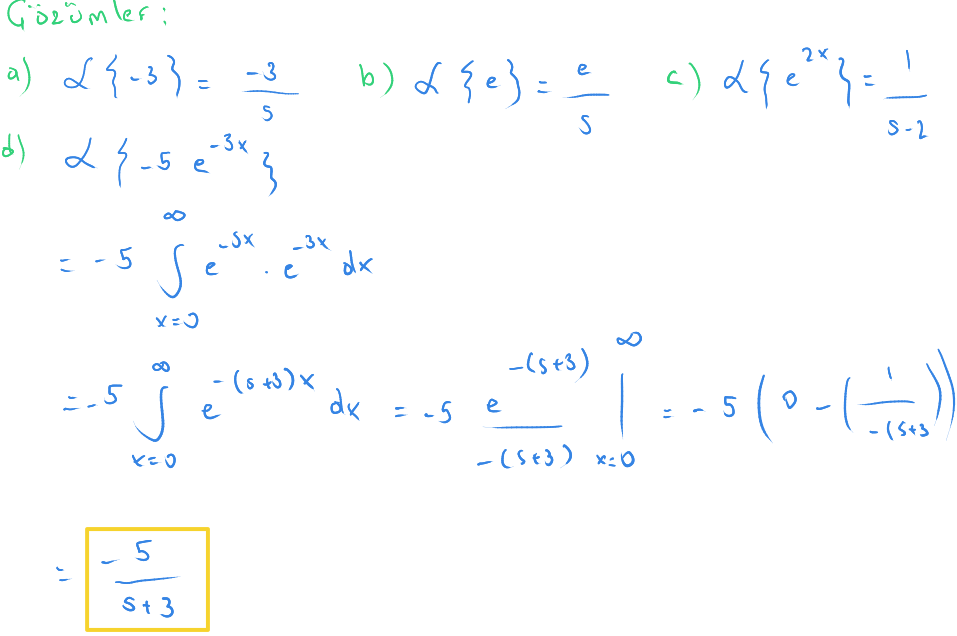
Dördüncü soruda temel Laplace tanımını kullandık.
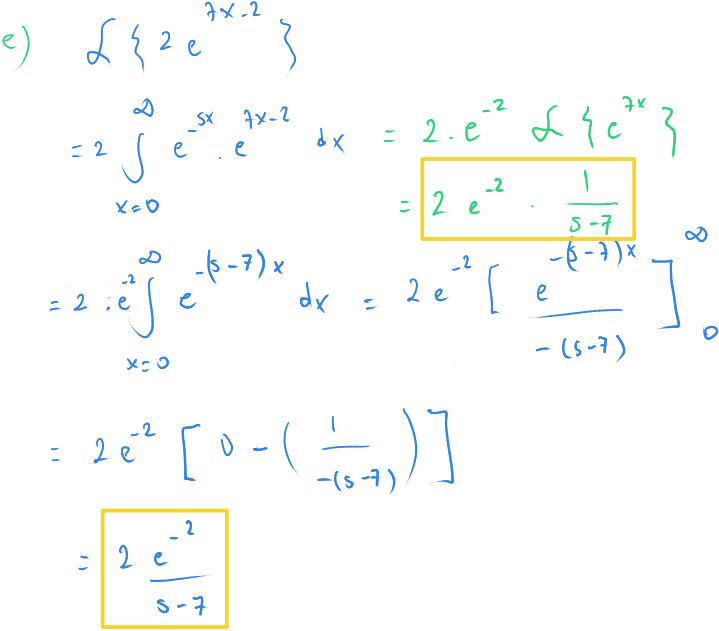
Beşinci soruyu hem kısa, hem uzun yöntemle çözdük.
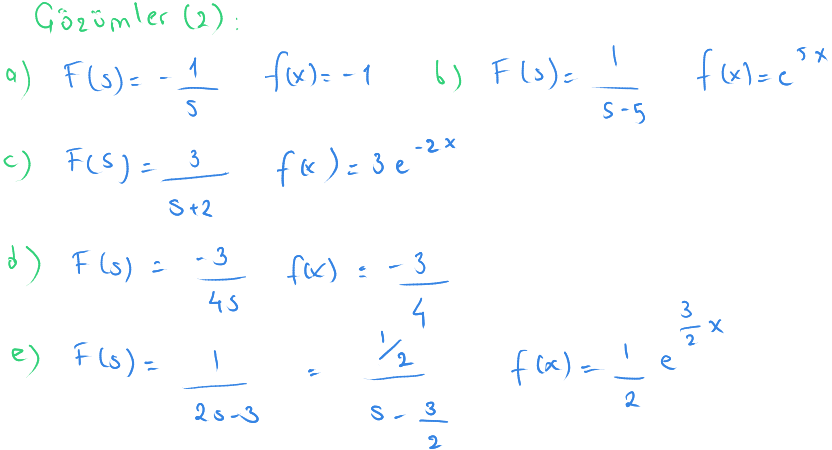
Son şıkta dikkat ederseniz payı ve paydayı bir sabitle çarptık.
Yorumlar