Laplace dönüşümü 2
Türevin Laplace dönüşümü
Türevin Laplace dönüşümü
Bir f(x) işlevinin Laplace dönüşümüne L{f(x)}=F(s) diyelim.
Bu işlevin türevinin f'(x) Laplace dönüşümünü hesaplayalım .

Burada kısmı integral yöntemini kullanıyoruz.
Dikkat ederseniz, türevin Laplace dönüşümünü hesaplamak isterken işlevin kendisinin Laplace dönüşümü L{f(x)}=F(s) karşımıza geliyor.
Laplace dönüşümünün iki özelliği
1 - Toplama ya da çıkarma içeren bir ifademiz olsun.
Bu ifadenin tamamının Laplace dönüşümü, parçaların ayrı ayrı Laplace dönüşümü alınarak toplanmasına eşittir.
$ L \{ f(x) \pm g(x) \} = L \{ f(x) \} \pm L \{ g(x) \} $
Ters Laplace dönüşümü için de bu kural geçerlidir.
$ L^{-1} \{ F(s) \pm G(s) \} = L^{-1} \{ F(s) \} \pm L^{-1} \{ G(s) \} $
2 - Bir sabit ile çarpım şeklinde bir ifademiz olsun. İfadenin tamamının Laplace dönüşümü, sabitle işlevin Laplace dönüşümünün çarpımına eşittir.
$ L \{ k f(x) \} = k L \{ f(x) \} $
Ters Laplace dönüşümü için de bu kuralı yazabiliriz.
$ L^{-1} \{ k F(s) \} = k L^{-1} \{ F(s) \} $
Örnek
Bu bilgilerle donandığımıza göre basit bir türevli denklem çözmeye çalışalım.
Burada hesapladığımız
$ L \{ f'(x) \} = s F(s) - f(0) $
kuralını kullanınız.
Çözümü bulmak için eşitliğin her iki tarafının Laplace dönüşümünü alınız.
Türevli denklem aşağıdaki gibidir.
$ f'(x) + f(x) = 1$ ve $f(0) = 0 $
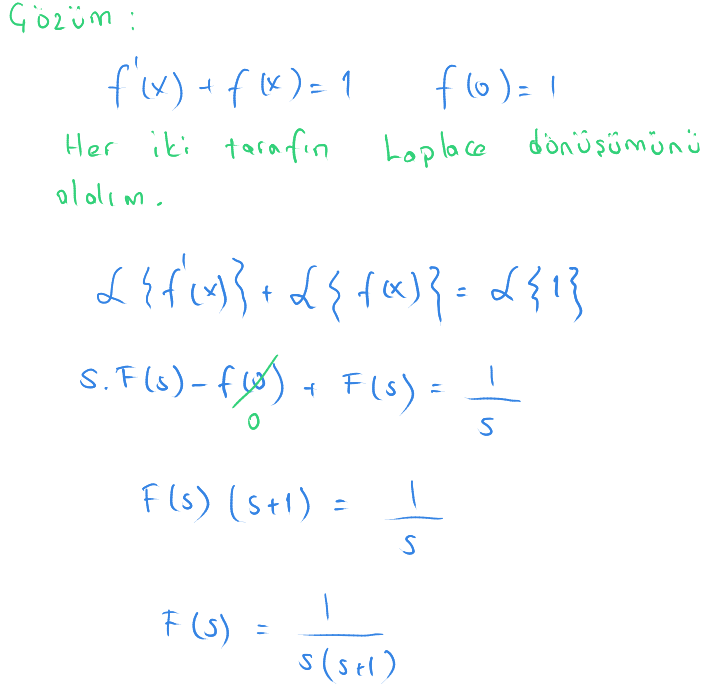
Bu ifadeyi kesirlere bölmemiz gerekiyor.
Kesirlere bölme için bu derse bakabilirsiniz.
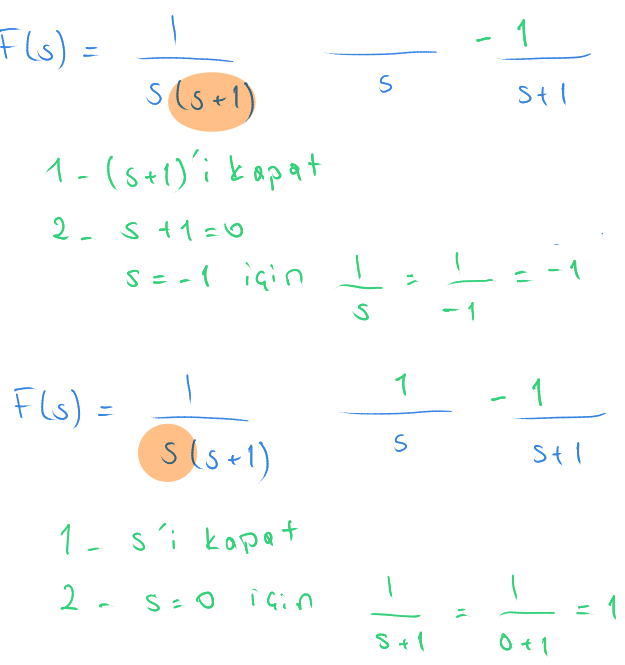
Gene de sizin için konunun özetini yaptım.

Böylece Laplace dönüşümü kullanarak ilk türevli denklemimizi çözmüş olduk.
Çok gerekli değil ama, isterseniz bu ilk örnek için matematik yazılımı kullanarak sağlamasını da yaptırabilirsiniz.
Laplace dönüşümü tablosu

Pekiştirme
Aşağıdaki türevli denklemleri çözünüz.
$ (a)\ f'(x) - f(x) = 2 $ ve $ f(0)=0 $
$ (b)\ f'(x) + f(x) = e^{-x} $ ve $ f(0)=0 $
$ (c)\ f'(x) + f(x) = 3 $ ve $ f(0)=-2 $
$ (d)\ f'(x) - f(x) = e^{2x} $ ve $ f(0)= 1 $
$ (e)\ 3 f'(x) - 2 f(x) = 4e^{-x} + 2 $ ve $ f(0)=0 $
Çözümler
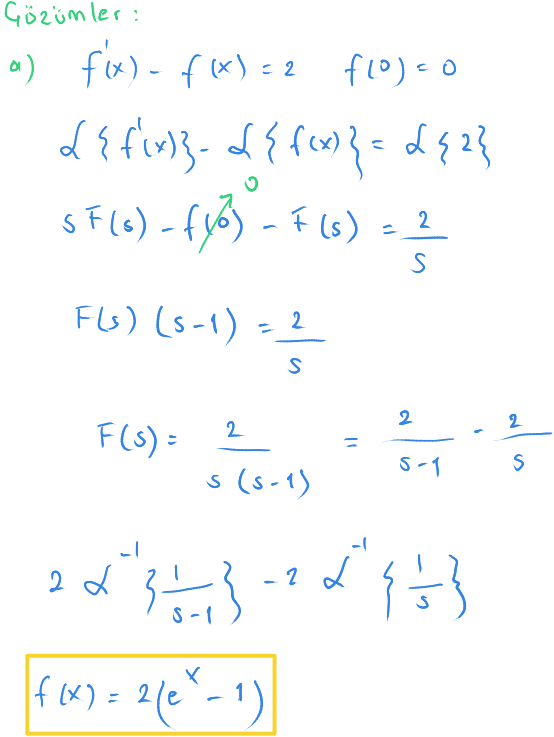
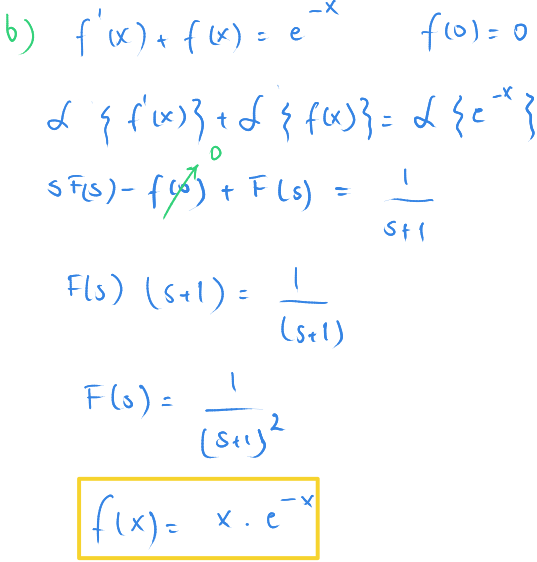
Bu örnekte tabloya son eklediğimiz kuralı kullanıyoruz.
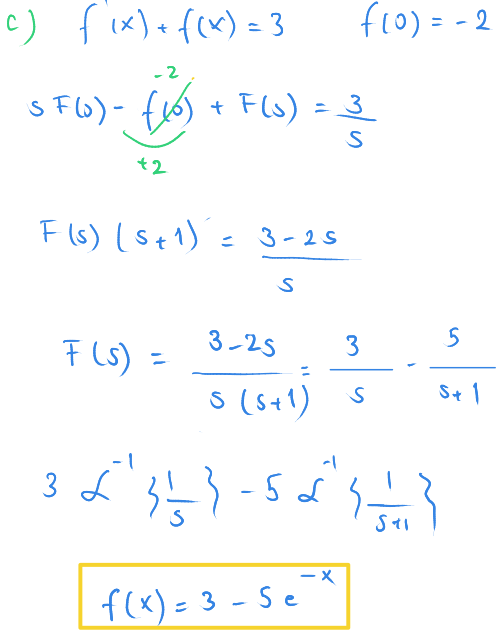
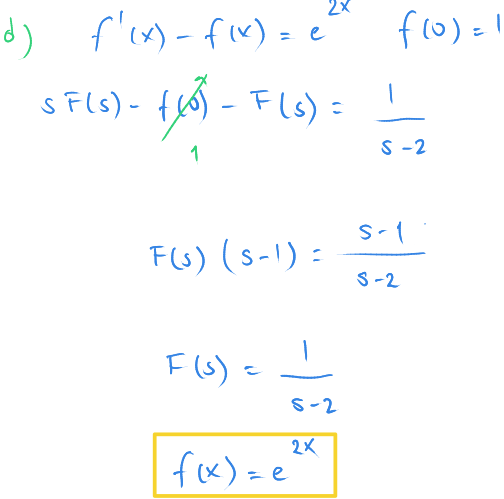
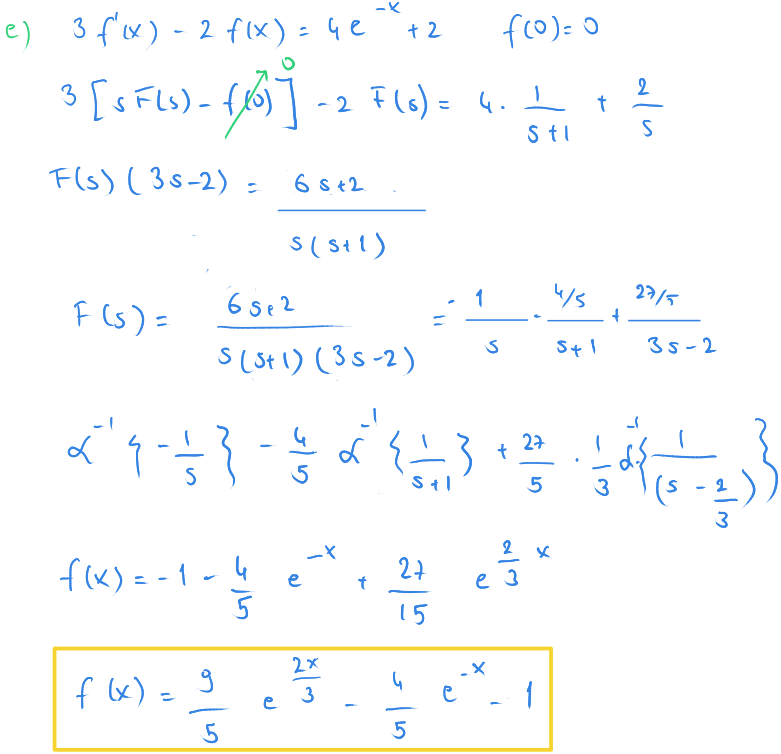
Yorumlar