Ortak kanallı yükselteç tam direnç ölçümü
Ortak kanallı yükselteç tam direnç ölçümü
Giriş
Bu derste ortak kanallı yükseltecin giriş ve çıkış tam direncini ilk önce hesaplayıp sonra ölçmeye çalışacağız.
Devre şeması
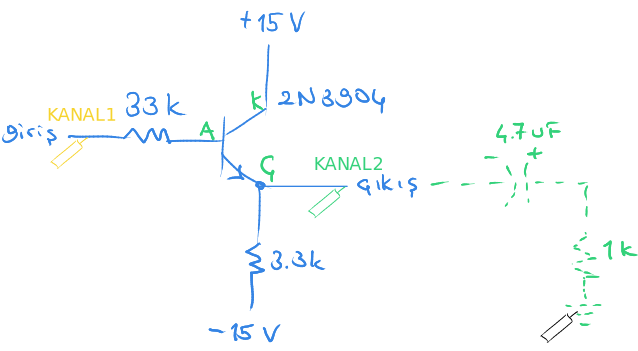
Devre şemasına baktığımızda daha önce görmüş olduğumuz çıkışı izleyen devresine çok benziyor.
Giriş çıkış tam direnci hesabı
Burada farklı bir yöntem izledik.
Ölçümü yapmadan önce giriş ve çıkış tam dirençlerini hesapladık.
Yaptığımız hesabın pratikle örtüşüp, örtüşmediğini merak ettik.
Transistörün tam direnç ve kazanç hesabını önceki derslerde anlatmıştık.
Akım kazancını hesaplamak için $I_A$ , $I_Ç$ akımlarını ölçeceğiz. Ayrıca transistörün $r_{iç}$ direncini de hesaplamamız gerekecek. İhtiyaç olmasa da $V_Ç$ gerilimini de ölçtük.
Bulduğumuz sonuçlar aşağıdaki gibidir.
$I_A = 4,11\,mA$
$I_Ç = 21\,uA$
$V_Ç = 13,24\,V$
Öncelikle ana vana ve çay üzerinden akımlara bakalım.
$I_Ç = (\beta+1) I_A$
Akım kazancını tek başına bırakırsak
$(\beta+1) = \frac {I_Ç} {I_A} = \frac {4110}{21}$
Buradan transistörün akım kazancını $\beta$ 195 olarak buluruz.
Transistörün iç direnci şu şekilde hesaplanıyor.
$ r_{iç} = \frac {26 mV} {I_{çıkış}}$
Değerleri yerine koyalım.
$ r_{iç} = \frac {26 mV}{4,11 mA} = 6 \,\Omega$
Şimdi devre şemasına tekrar bakabiliriz.
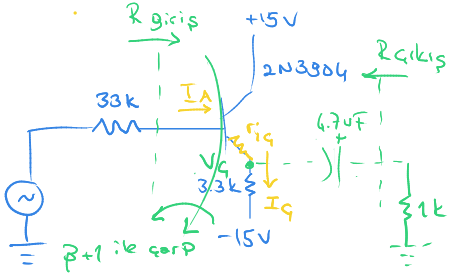
Burada 33 K direnç devrenin bir parçası değildir.
Ana vana üzerinden bir çizgi çekiyoruz. Bunu bir duvar olarak düşünebiliriz.
Duvarın soluna aktardığımız değerleri $(\beta+1)$ ile çarpıyoruz.
$R_{giriş}$ ten ok yönünde devam ettiğimizde $r_{iç}$ ve buna seri 3,3 K direnç olduğunu görebiliriz.
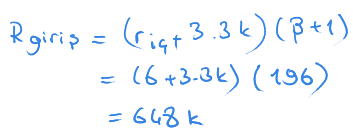
Bunları sola aktardığımızda devrenin giriş tam direncini 648 K bulduk.
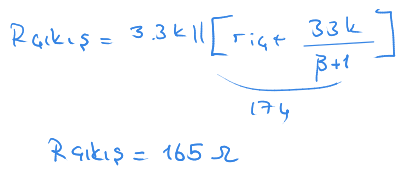
Çıkış tam direncini bulurken $R_{çıkış}$ tan ok yönünde devam ettiğimizde bir kol 3,3 K olarak ayrılıyor. Diğer kol ise $r_{iç}$ ile başlıyor ama buna seri direnç de var.
Buradan çıkış direncini $165 \Omega$ olarak hesapladık.
Giriş tam direnci ölçümü
Giriş tam direncini hesaplamak için girişten büyüklüğü 800 mV olan sinüs şeklinde 1 kHz bir işaret göndereceğiz. Sonra çıkış işaretinin büyüklüğüne bakacağız.
33k direnci daha büyük dirençlerle değiştireceğiz ve çıkışa bakacağız. Çıkıştaki işaret küçülmeye başlayacak.
Çıkış işaretinin büyüklüğü % 50 azaldığında kullandığımız $R$ direnci, giriş tam direncine eşit $R_{giriş}$ eşit olacak.
Ölçümü kolay yapabilmek için her iki kanalı AC'ye bağlayabiliriz.
Eğer osiloskobunuzda büyüklük ("amplitude") ölçme özelliği varsa bundan faydalanabilirsiniz.
Ölçümler
Ölçüme önce 33 K dirençle başlıyoruz.
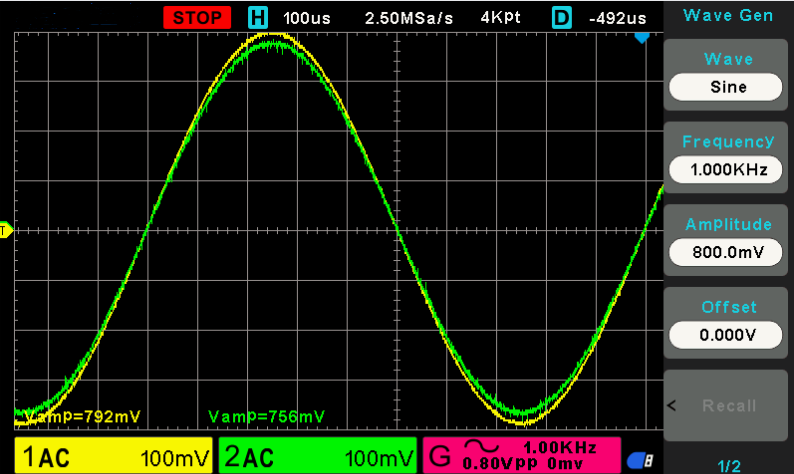
Görülebileceği üzere 40 mV kadar bir azalma var.
Daha sonra 100 K, 220 K, 470 K dirençlerle de denedik.
En sonunda 690 K direnç kullandık.
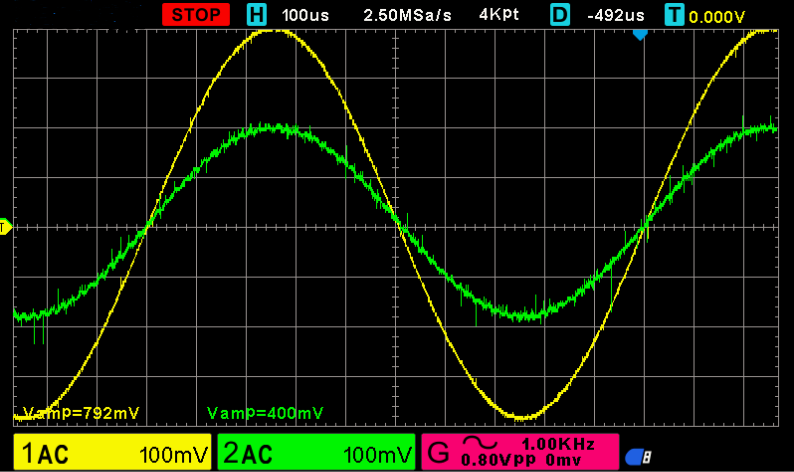
Dikkat ederseniz giriş işareti yarıya düştü.
Girişte 800 mV verip çıkışta 400 mV gördük.
Buradan devrenin giriş tam direncinin yaklaşık 690 K olduğunu söyleyebiliriz.
Çıkış tam direnci ölçümü
Çıkış tam direnci ölçümü için transistörün ana ucuna tekrar 33 K direnç takıyoruz.
Devre bu halde iken çıkış geriliminin büyüklüğünü ölçüyoruz.
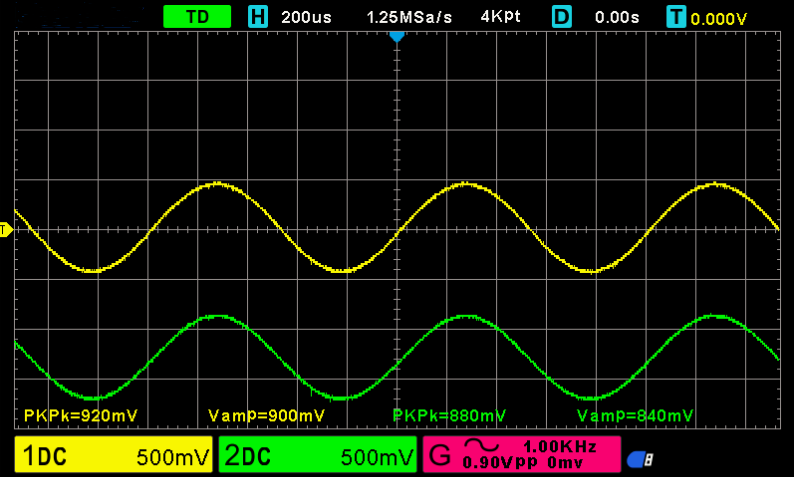
Yeşil ile gösterilen çıkış işaretinin büyüklüğünü öğreniyoruz. Görülebileceği üzere 840 mV dur.
Daha sonra yük halinde çıkış işaretini ölçmek için 4,7 uF sığaç ve 1 k yük direnci ekliyoruz. Devrenin son hali aşağıdaki gibidir.
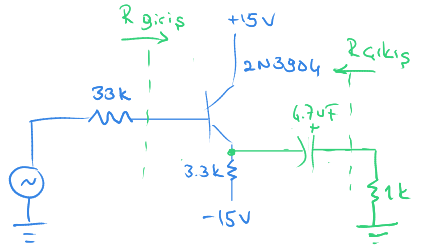
Burada farketmemiz gereken husus $R_{çıkış}$ ve 1k yük direnci bir gerilim bölücü oluşturuyor.
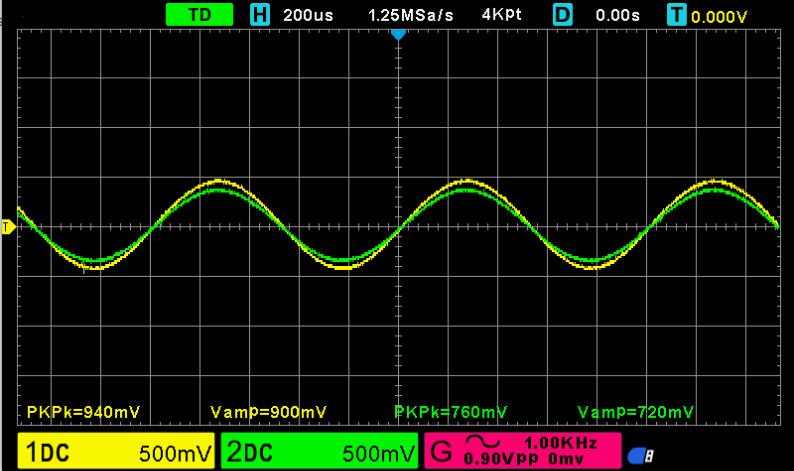
Devre yükte iken, yeşil ile gösterilen çıkış geriliminin büyüklüğü 720 mV oldu.
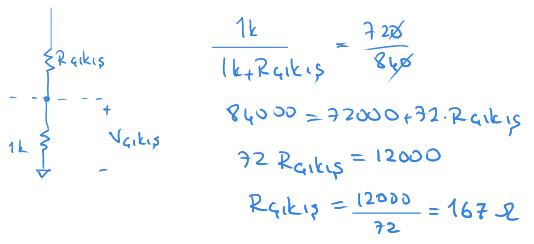
Gerilim bölücüyü çözersek $R_{çıkış}$ değerini $167 \Omega$ olarak buluruz.
Dikkat ederseniz ölçerek bulduğumuz bu değer, üstte hesaplayarak bulduğumuz değere çok yakındır.
Yorumlar