Transistör tam direnç kazanç hesabı
Transistör tam direnç kazanç hesabı
Giriş
Bu derste transistör tam direnç, kazanç hesaplarına bakacağız.
Burada elektronikte kullanılan direnç isimlerinden bahsetmiştik.
Giriş tam direnci
Öncelikle aşağıdaki devreye bakalım.
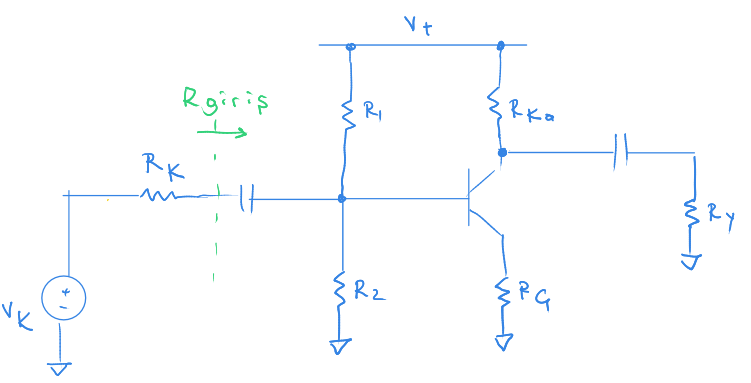
Burada $R_{giriş}$ i bulmaya çalışacağız.
Dalgalı akım hesabı yaptığımız için tüm doğru akım kaynakları kısa devre olacak. V+ toprak olacak.
Hesap yapmak istemiyorsak $R_{giriş} = R_1\,||\,R_2$ dersek giriş tam direnci için yakın bir tahminde bulunabiliriz.
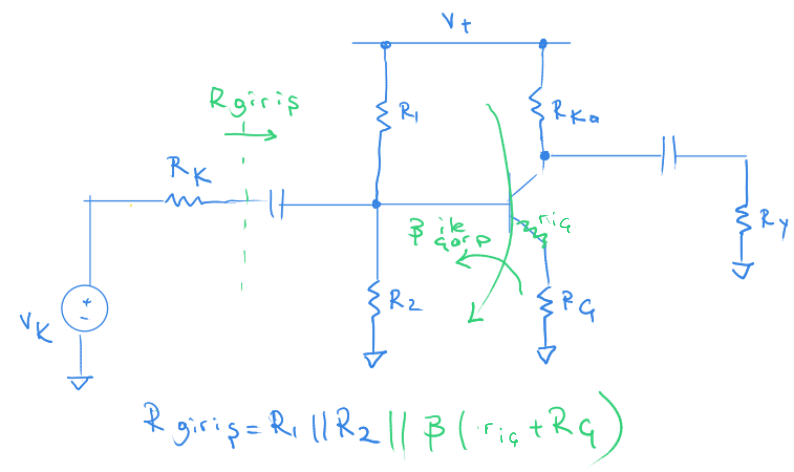
Eğer hesabımız tam olsun istiyorsak transistörün ana vanasından yeşille gösterilen bir çizgi çekiyoruz. Bunu bir duvar gibi düşünebiliriz.
Duvarın sağ tarafında $R_Ç$ ile seri durumda transistörün iç direnci olan $r_{iç}$ var.
Bu ikisi birbirine seri olduğu için bunları topluyoruz.
Duvarın soluna attıklarımızı transistörün akım kazancı $\beta$ ile çarpıyoruz.
Örnek 1
Aşağıdaki devrenin giriş tam direncini hesaplayalım.
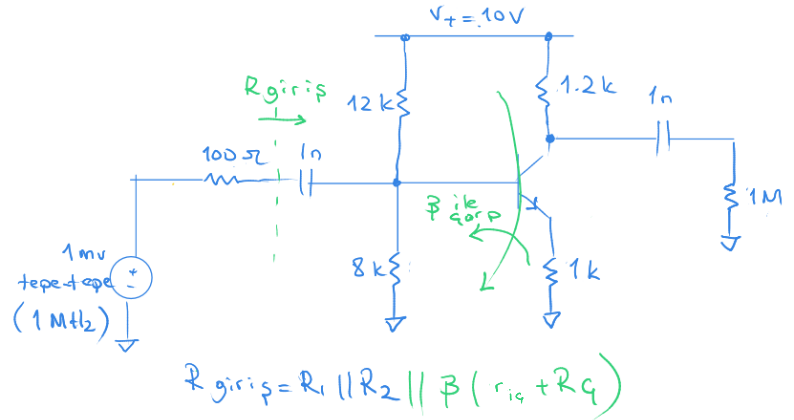
Bahsettiğimiz gibi kabaca giriş tam direncine $R_{giriş} = 12k\,||\,8k$ dersek giriş tam direnci için yakın bir tahminde bulunabiliriz.
Paralel direnç hesabı için bu hesap tablosundan faydalanabilirsiniz.
Kabaca hesap yaptığımızda giriş tam direncini yaklaşık 4.8 k buluyoruz.
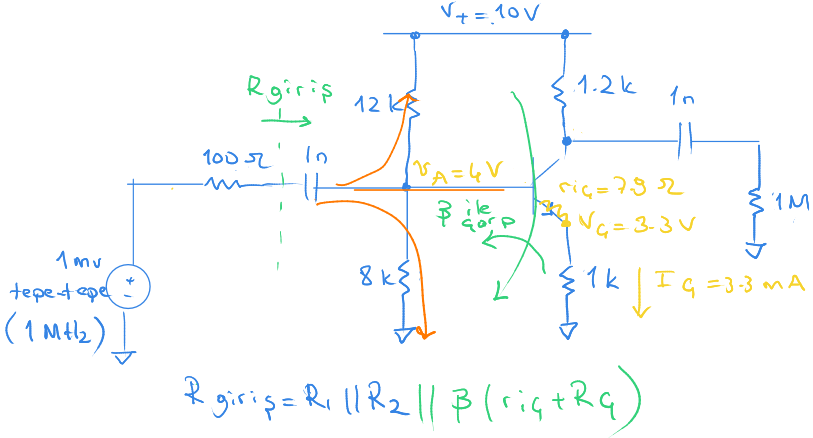
Ayrıntılı hesaba ana vana üzerindeki gerilimi bulmakla başlayalım.
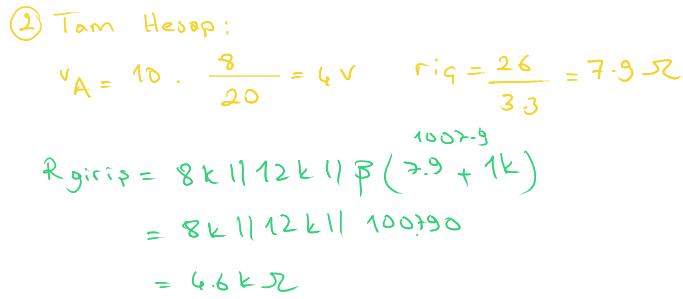
$V_{çıkış}$ gerilimi ana vana üzerindeki gerilimden yaklaşık 0,7 volt düşük olacak. Böylece değerini 3,3 volt bulduk.
Çıkış akımı 3.3 mA dir.
İç direnci oda sıcaklığında 26 sabit sayısını çıkış akımına bölerek bulabiliyoruz.
Giriş tam direnci tarafından geldiğimizde 12k, 8 k ve ana vanaya giden olmak üzere üç kola ayrılıyor.
Ana vananın tam üzerinden geçen yeşil çizgiyi bir duvar olarak kabul edebiliriz.
$r_{iç}$ ve buna seri 1k direnci, duvarın üzerinden sola atlatırken $\beta$ ile çarpıyoruz.
Böylece sonucu 4,6 k olarak bulduk.
Bulduğumuz sonucun, kabaca yaptığımız hesaba çok yakın olduğunu görebilirsiniz.
Örnek 2
Aşağıdaki devrenin giriş tam direncini hesaplayalım.
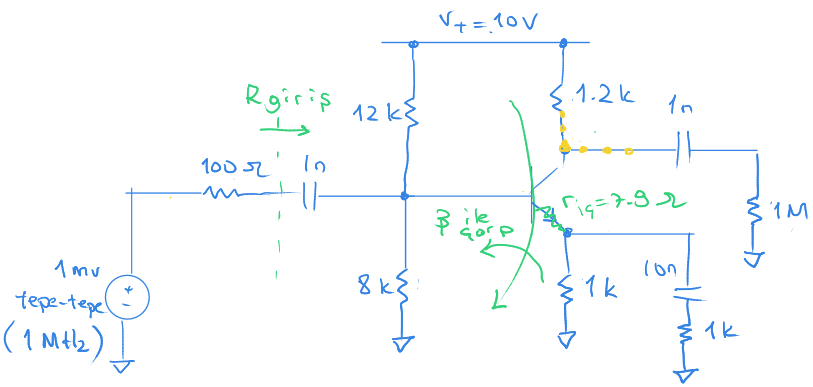
Bu örnek bir önceki örneğe çok benziyor.

Burada görmemiz gereken, dalgalı akım hesabı yaptığımız için 10 k direncin ucundaki 10n sığaç kısa devreye düşüyor.
Böylece hesaplamada $r_{iç}$ direncine seri iki tane paralel 1k direnç oluyor.
Örnek 3
Aşağıdaki devrenin giriş tam direncini ve gerilim kazancını hesaplayınız.
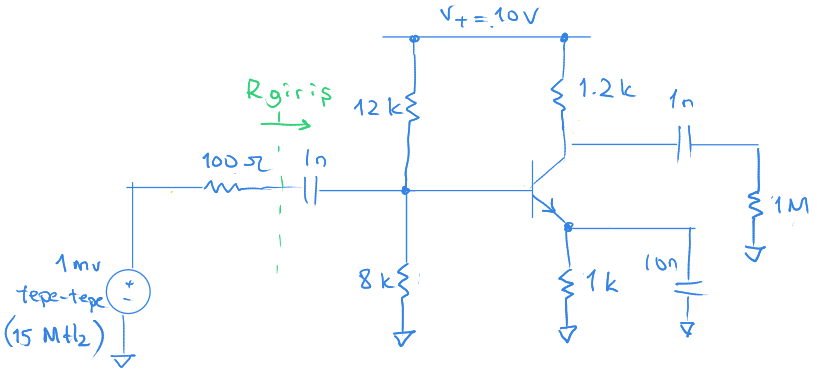
Bu örnek önceki örneklere benziyor. Ancak ufak bir püf nokta var.
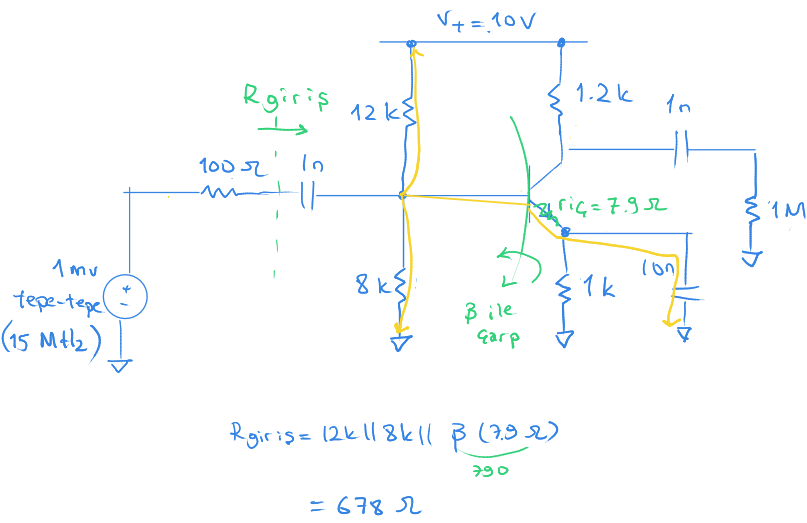
$R_{giriş}$ tarafından baktığımızda 12 k bir kola, 8 k bir kola ayrılıyor. Bir de bu ikisine paralel bir kol var. Bu kola baktığımızda $r_{iç}$ e seri 10 n sığaç nedeniyle kısa devre oluyor.
Böylece giriş tam direncini sadece 678 Ω bulduk.
Dalgalı akım devre modelini çizelim.
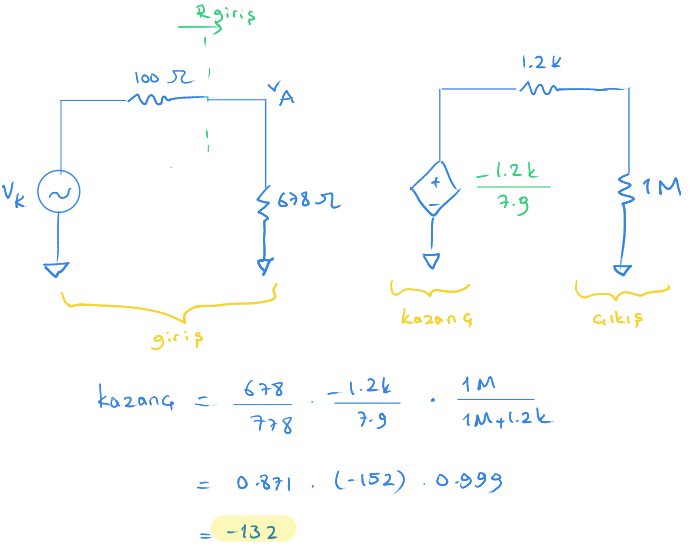
Girişte $V_A$ gerilimini basit bir gerilim bölücü ile bulabiliriz.
Kazanç bölümünde baklava dilimine benzeyen şey bir akım kaynağıdır. Transistörü dalgalı akımda modellerken bir akım kaynağı olarak modelliyoruz.
Burada kazanç, kanal direncinin $R_{Ç}$ direncine oranından bulunuyor. $r_{iç}$ direncine seri 1k direnç, 10 n sığaç tarafından kısa devre yapıldığı için hesaba katılmıyor.
Çıkış katında gene bir gerilim bölücü bulunuyor.
Hesabı yaptığımızda kazancı yaklaşık -132 olarak buluyoruz.
Örnek 3 devre benzetimi
Bu örnekleri yapıyoruz ama gerçekte çalışır mı diye düşünenler olabilir.
Bu nedenle bu örnek için LTSpice devre benzetim kütüğünü paylaşıyoruz.
Çıkış tam direnci
Aşağıdaki devreye bakalım.
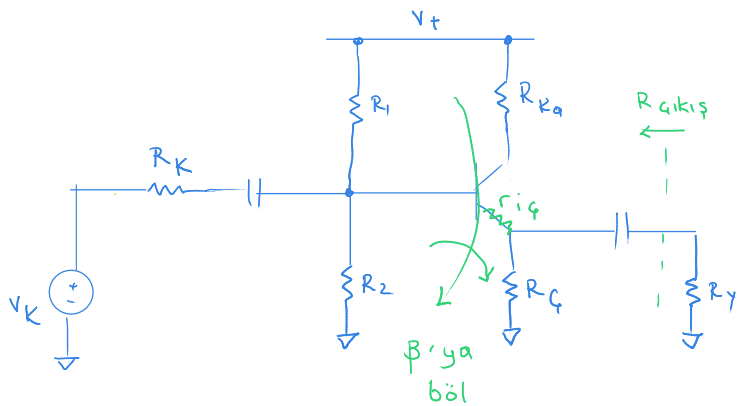
Bu sefer $R_{çıkış}$ ı bulmaya çalışacağız.
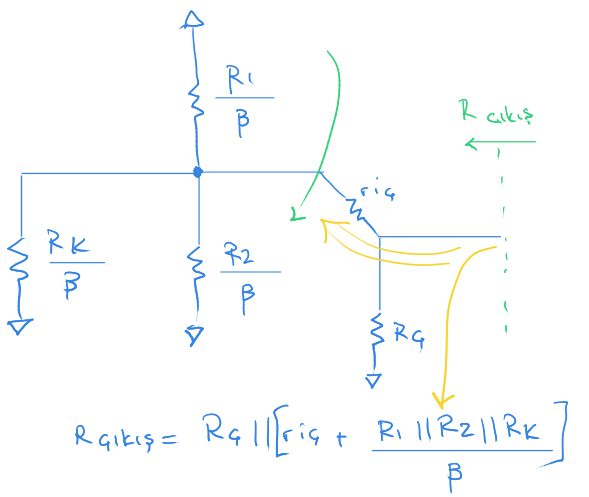
Transistörün ana vanasından yeşil bir çizgi çekiyoruz. Bunu bir duvar olarak düşünebiliriz. Duvarın sağına aktardıklarımız $\beta$ 'ya bölüyoruz.
$R_{çıkış}$ tan sola doğru geliyoruz. Hemen $R_Ç$ direnci var. Buna paralel $r_{iç}$ direnci var. Diğer tüm dirençlerin $r_{iç}$ direncine seri olduğu görülebilir. Bu nedenle diğerlerini topluyoruz.
Diğer dirençleri çizginin sağına aktarırken $\beta$ 'ya bölüyoruz.
Yorumlar